Edmond Halley (1716), Philosophical Transactions, 29, 454-465
Methodus singularis, quâ Solis Parallaxis sive distantia à Terra, ope Veneris intra Solem conspiciendae, tuto determinari poterit ; proposita coram Regia Societate ab Edm. Halleio J. U. D. ejusdem Societatis Secretario.
(Traduit du latin par Elisabeth Bonche et Michel Toulmonde. Remerciements à Michel Lerner pour la relecture. Notes de Michel Toulmonde).
Méthode singulière pour déterminer sûrement la parallaxe du Soleil ou sa distance à la Terre par les observations de Vénus dans le Soleil, proposée devant la Royal Society par Edmond Halley, Docteur dans les Deux Droits, secrétaire de la Société.
Il y a d'innombrables propositions extrêmement paradoxales et qui dépassent toute créance chez les gens ordinaires, que l'on peut pourtant assez facilement résoudre à l'aide de principes mathématiques. Or il ne semble pas y avoir de problème plus ardu et difficile que de déterminer la distance du Soleil à la Terre en serrant au plus près la vérité ; pourtant, si l'on recueille certaines observations, faites avec grand soin à des dates précises définies par avance, on pourra y parvenir sans grand effort. Tels sont les éléments que je tiens à exposer à notre illustre Société, à laquelle je prédis un avenir immortel. Ma communication est particulièrement destinée aux plus jeunes de nos astronomes qui, nés plus tard, auront peut-être la chance de faire les observations dont je parle ; puissé-je leur ouvrir la voie qui leur permettra de calculer avec rigueur la distance immense qui nous sépare du Soleil, à un 500e près.
Or, vous le savez, les divers astronomes qui font autorité donnent de cette distance une estimation variable selon la conjecture adoptée par chacun. D'après Ptolémée et ceux qui le suivent, comme d'après Copernic et Tycho Brahe, elle est égale à 1200 fois le demi-diamètre de la Terre ; selon Kepler 3500 fois. Riccioli double le chiffre de Kepler, qu’Hevelius, pour sa part, n’augmente que de moitié. Mais depuis que l’on a pu, à l’aide de la lunette, voir sur le disque du Soleil les planètes Vénus et Mercure dépouillées de leur éclat d’emprunt, on a fini par se rendre compte que le diamètre visible de ces planètes est bien inférieur à ce que l’on pensait jusque là ; que le demi-diamètre de Vénus vu depuis le Soleil vaut au plus le quart d’une minute soit 15" ; que le demi-diamètre de Mercure à sa distance moyenne du Soleil s’observe sous un angle de 10" seulement ; et que c’est également sous un angle de 10" qu’est vu le demi-diamètre de Saturne depuis le Soleil. En ce qui concerne le demi-diamètre de Jupiter, la plus grande des planètes, il vaut seulement un tiers de minute [20"] depuis le Soleil. Il a donc semblé à certains des astronomes modernes, par analogie, que le demi-diamètre de la Terre, lui aussi observé depuis le Soleil, a une valeur intermédiaire entre celui de Jupiter, plus grand, et ceux de Saturne et de Mercure, plus petits, et qu’il est égal à celui de Vénus, à savoir 15" : et surtout que la distance du Soleil à la Terre est d’environ 14 000 fois le demi-diamètre de la Terre. Mais les mêmes auteurs, pour une autre raison, ont augmenté légèrement cette distance ; en effet, puisque le diamètre de la Lune est un peu supérieur au quart de celui de la Terre, si on posait l’hypothèse d’une parallaxe du Soleil de 15", le globe lunaire serait plus grand que celui de Mercure et donc une planète à l'évidence secondaire [un satellite] serait plus grande qu’une planète primaire : ce qui semblerait contraire à la disposition ordonnée du système du monde. Tout à l’inverse, cette même disposition semble difficilement laisser admettre que Vénus, planète inférieure [intérieure] et dépourvue de tout satellite, soit plus grande que notre Terre qui est, elle, supérieure et dotée d’une compagne aussi remarquable. On peut donc supposer, pour prendre une valeur intermédiaire, que le demi-diamètre de la Terre vu depuis le Soleil, ou bien, ce qui revient au même, la parallaxe horizontale du Soleil, a une valeur de 12" 1/2 : il en résulte que la Lune sera plus petite que Mercure, et la Terre plus grande que Vénus ; et, par voie de conséquence, la distance du Soleil à la Terre à peu de chose près 16 500 fois le demi-diamètre de la Terre. C’est à cette valeur que je me range pour l’instant, en attendant que sa mesure exacte puisse être établie avec certitude grâce à l'expérience que nous présentons. Et, quel que soit le prestige de leur autorité, je ne m'attarde pas aux thèses de ceux qui repoussent à l’infini, bien au-delà de ces limites, la distance qui nous sépare du Soleil, se fondant sur l’observation des oscillations d’un pendule pour déterminer de minuscules fractions d’angles, évidemment trop peu fiables. En tout cas, si quelqu’un tente d'essayer cette méthode, il trouvera pour la parallaxe une valeur parfois nulle ou même parfois négative ; c’est-à-dire que la distance deviendra ou bien infinie, ou bien plus grande que l’infini : ce qui est absurde. Et, à dire vrai, c'est à peine si l'homme est capable de distinguer avec certitude des secondes [de degré] ou même 10" à l’aide d’instruments, aussi habilement fabriqués soient-ils ; et il n’y a rien d’étonnant que les multiples tentatives ingénieuses de tant d’habiles techniciens se soient trouvées déjouées jusqu’à présent par l’extrême ténuité de la mesure même à effectuer.
Il y a près de 40 ans [en 1677], tandis que je me consacrais, sur l’île de Sainte-Hélène, à l’observation des astres qui entourent le pôle Sud, j’ai eu la chance d’observer avec la plus grande attention le passage de Mercure sur le Soleil : et, circonstance en laquelle j’ai bénéficié d’une chance inespérée, j’ai pu saisir en toute rigueur l’instant où Mercure, pénétrant sur le disque solaire, est apparu à l’intérieur de celui-ci, juste en contact avec le limbe ; de la même façon, j’ai pu saisir l’instant où, sortant [du disque solaire], il a touché intérieurement le limbe du Soleil. Ces observations, je les dois à mon excellente lunette de 24 pieds [7,3 m]. A la suite de cela, j’ai pu établir de façon certaine la durée au cours de laquelle Mercure est apparu tout entier à l’intérieur du disque du Soleil, sans même une erreur d’une seconde de temps ; en effet, le filament de lumière solaire qui démarquait le bord obscur de la planète du bord lumineux du Soleil, bien qu’extrêmement ténu, a été distinctement visible ; et j’ai vu en un clin d'œil la petite encoche formée dans le bord du Soleil par l’entrée de Mercure s'effacer, de même que j’ai vu celle de la sortie de Mercure naître pour ainsi dire dans l'instant. A la vue de ce phénomène, j’ai compris tout de suite que l’on pourrait déduire avec rigueur la parallaxe du Soleil en partant d’observations de cet ordre, si seulement Mercure, plus proche de la Terre, avait une parallaxe bien plus grande que celle du Soleil ; en fait, cette différence entre les parallaxes est si faible qu’elle est toujours plus petite que celle du Soleil que nous cherchons à trouver ; c'est pourquoi Mercure, qui est pourtant visible souvent sur le Soleil, sera considéré comme peu adapté à notre entreprise.
Il reste donc le cas du passage de Vénus sur le disque du Soleil ; environ quatre fois plus grande que celle du Soleil, sa parallaxe produira des écarts tout à fait perceptibles entre les diverses durées du parcours de Vénus à travers le Soleil si on l'observe depuis différents endroits de notre Terre. Or, à partir de ces écarts observés de façon convenable, j’affirme qu’il est possible de déterminer la parallaxe du Soleil avec une précision d’une petite fraction de seconde de degré. Et nous n'avons pas besoin d'autres instruments qu'une lunette et une horloge ordinaires mais de bonne qualité ; en ce qui concerne les observateurs, tout juste de la rigueur et du soin avec un bagage modéré en astronomie. Il n’est pas nécessaire en effet de chercher de façon méticuleuse la latitude du lieu ni de déterminer avec précision l'heure du méridien [la longitude] : il suffit, après avoir réglé correctement les horloges sur les mouvements célestes, de mesurer l’intervalle de temps qui s’écoule entre l’entrée totale de Vénus à l’intérieur du disque solaire jusqu’au début de sa sortie hors de ce disque - ce qui signifie dès que le globe sombre de Vénus commence à toucher le bord lumineux du Soleil ; ces instants, je le sais par expérience personnelle, peuvent être observés à la seconde de temps près.
Or, en raison des lois qui régissent très étroitement le cours des planètes, il est extrêmement rare que l’on puisse observer Vénus à l’intérieur du disque du Soleil et, sur une durée de plus de 120 ans, on ne la verra même pas une seule fois ; précisément, depuis 1639 (date à laquelle notre jeune et illustre compatriote Horrocks a eu la chance, le seul et le tout premier depuis que le monde existe, d’assister à ce spectacle merveilleux) jusqu’à l’année 1761, date à laquelle, selon les théories dont nous avons jusqu’à présent vérifié la concordance avec les mouvements célestes, l’étoile Vénus viendra traverser à nouveau le Soleil, le 26 mai au matin [1] ; de telle sorte que, à Londres, il faut l’attendre au milieu du disque solaire vers 6 heures du matin et à moins de 4' au sud du centre du Soleil. Quant à la durée de sa traversée, elle sera d’environ huit heures, à savoir de 2h à 10h du matin environ. Au reste, son entrée ne sera pas visible en Angleterre : mais comme le Soleil se trouvera à ce moment-là à 16° des Gémeaux avec une déclinaison boréale de 23° environ, elle sera observable dans pratiquement toute la zone froide septentrionale où le Soleil ne se couche pas : par conséquent les habitants des côtes de la Norvège situées au-delà de la ville de Nidrosia, qu’ils appellent Dront [Trondheim], jusqu’au cap septentrional de ce pays pourront observer l’entrée de Vénus sur le disque du Soleil ; et peut-être cette entrée pourra-t-elle aussi être observée, au lever du Soleil, par les habitants du Nord de l’Ecosse et par ceux de l'île Hetlandia [Shetland], appelée autrefois Thulé. Mais à ce moment, Vénus sera au plus près du centre du Soleil, le Soleil sera à la verticale des rives Nord du golfe du Gange, ou même plutôt du royaume de Pegu [Birmanie] ; et par conséquent, dans les régions voisines, comme le Soleil, au moment de l’entrée de Vénus, sera environ à quatre heures de son lever, tout comme il sera également à quatre heures de son coucher au moment de la sortie de Vénus, le mouvement apparent de Vénus à l’intérieur du Soleil sera accéléré d’une valeur approximativement égale au double de la parallaxe horizontale de Vénus au Soleil ; car, à ce moment-là, Vénus est entraînée d’Est en Ouest par un mouvement rétrograde, tandis qu’un œil situé à la surface de la Terre tourne en sens contraire, d’Ouest en Est.
Si l’on pose pour la parallaxe du Soleil, comme nous l’avons dit, la valeur de 12" 1/2, la parallaxe de Vénus sera de 43" [2] ; si l’on en soustrait la parallaxe du Soleil, il restera au moins une demi-minute de degré [30"] pour la parallaxe horizontale de Vénus au Soleil et donc le mouvement de Vénus, en raison de sa parallaxe, sera accéléré de trois quarts de minute [45"] pendant sa traversée du disque solaire [observée] aux latitudes qui sont voisines du Tropique, et plus encore dans les environs de l’Équateur. Vénus, à ce moment-là, accomplira son parcours sur le Soleil à la vitesse assez exacte de 4' par heure ; et, aux trois quarts de minute de degré correspondent en proportion 11 minutes [3] dont est réduite la durée du passage, à cause de la parallaxe de Vénus. Et cette réduction de la durée pourrait seule permettre de trancher en toute certitude sur la question de la parallaxe que nous cherchons, sous réserve que le diamètre du Soleil et la latitude de Vénus nous soient donnés avec une très grande précision ; toutefois, demander un calcul exact sur une matière aussi délicate à évaluer n'est pas raisonnable.
Il faut donc se procurer une autre observation ailleurs, si cela peut se faire, dans les endroits où Vénus occupe le milieu du Soleil à minuit ; ainsi sous le méridien opposé au précédent, c’est-à-dire à six heures ou à 90° à l’Ouest de Londres, où Vénus entre sur le disque solaire peu avant son coucher et en sort peu après son lever ; ceci se produira sous le méridien en question, à une latitude d’environ 56° Nord, dans un lieu appelé Baie d’Hudson, vers le port baptisé Nelson. En effet, à proximité de cet endroit, la parallaxe de Vénus augmentera la durée de son passage d’au moins 6 minutes ; car, pendant qu'on verra le Soleil passer sous le Pôle dans sa course du coucher au lever, ces lieux sur le globe terrestre se verront emporter vers l'Ouest, par un mouvement opposé, sous l’effet combiné de la rotation de la Terre et du mouvement propre de Vénus ; on verra donc Vénus progresser plus lentement à l’intérieur du Soleil et en traverser le disque en une durée plus longue.
C’est pourquoi, si l’on parvient à faire observer correctement ce passage de Vénus par des opérateurs compétents dans l’un et l’autre lieu, il est clair que la durée du passage observé à Port Nelson sera supérieure de 17 minutes à celle que l’on peut attendre aux Indes orientales ; et peu importe que ces mesures soient relevées à Fort Saint-George, appelé ordinairement Madras, ou à Bencoolen [Bengkulu] sur la côte ouest de l’île de Sumatra près de l’Equateur, si ce sont les Anglais qui, à ce moment-là, ont à cœur de l’étudier. Si ce sont les Français qui décident de s’y consacrer, l’observateur se placera commodément à Pondichéry sur la rive occidentale du Golfe du Bengale à une latitude de 12°. Quant aux Bataves, leur très célèbre ville de marché Batavia leur offre un lieu d’observation tout à fait adapté à cette entreprise, pour autant qu’ils aient eux aussi la volonté de faire progresser la science astronomique sur ce point. Et je voudrais vraiment que l’on puisse réaliser en différents lieux des observations du même phénomène, effectuées par des opérateurs nombreux : d’une part le consensus viendrait renforcer encore les certitudes sur ce sujet ; d’autre part cela éviterait qu’un passage nuageux ne vînt priver un observateur unique d’un spectacle que je ne sais si les hommes de ce siècle ni du suivant auront à nouveau l’occasion de voir, et dont dépend la solution exacte et décisive d’un problème particulièrement notoire, impossible à aborder par aucune autre voie. C’est pourquoi, aux astronomes curieux, à qui est réservée l’observation de tout cela, quand nous-mêmes ne serons plus, nous recommandons sans relâche de garder en mémoire l’appel que nous formulons ici et d’investir la totalité de leurs forces vives dans l’accomplissement de cette observation ; nous leur souhaitons très vivement d’avoir toutes les circonstances favorables, et en premier lieu de ne pas être privés, par l’obscurcissement inopportun d’un ciel nuageux, d’un spectacle si exceptionnellement attendu ; enfin que la gloire d’avoir défini avec une plus grande exactitude les dimensions des orbites célestes leur vaille une renommée éternelle.
Or nous avons dit que, selon cette méthode, la parallaxe du Soleil pouvait être calculée à un 500e près, ce qui en étonnera certainement plus d’un. Pourtant, si l’observation est conduite avec soin dans chacun des deux lieux qui ont été définis ci-dessus, nous avons déjà montré qu’il y aurait un écart de 17 minutes entre les durées de ces éclipses dues à Vénus, bien évidemment dans l’hypothèse où la parallaxe du Soleil aura été de 12" 1/2. Or, si on découvre à l’observation que cette différence est plus grande ou plus petite, la parallaxe du Soleil sera, à peu près dans la même proportion, plus grande ou plus petite. Et puisqu'une durée de 17 minutes correspond à 12" 1/2 pour la parallaxe du Soleil, chaque seconde de parallaxe donnera une différence de durée de plus de 80 secondes [4] ; par suite, si on a une différence sûre et certaine de moins de deux secondes, la parallaxe du Soleil s’établira au quarantième de seconde de degré près ; et, à partir de là, sa distance sera déterminée avec une erreur inférieure au 500e, à condition du moins qu’on ne trouve pas pour la parallaxe une mesure inférieure à celle que nous avons supposée : en effet 40 fois 12 1/2 font 500. [5]
Il me semble avoir donné désormais suffisamment d’indications et même au-delà aux astronomes avertis, à qui je voudrais également rappeler que je n’ai pas tenu compte, dans ce raisonnement, de la latitude de la planète, d’une part pour éviter les lourdeurs d’un calcul compliqué, qui ne conduiraient qu’à obscurcir la conclusion, d’autre part à cause du mouvement des nœuds de Vénus qui n’est pas encore connu et ne peut être déterminé correctement que par de semblables conjonctions de cette planète avec le Soleil. En effet, on n'a pu conclure que Vénus traversera le Soleil à 4' en dessous du centre qu’en admettant pour hypothèse que le plan de l’orbite de Vénus, immobile parmi la sphère des étoiles fixes, aura ses nœuds aux endroits mêmes où on les a découverts en 1639. Mais si Vénus devait suivre en 1761 une trajectoire plus au Sud, il apparaîtra clairement que ses nœuds ont reculé ; si au contraire elle suivait une trajectoire plus au Nord, il apparaîtra qu’ils ont avancé parmi les étoiles fixes ; et ceci à raison de 5' 1/2 en cent années juliennes pour chaque minute d’écart dans la distance de Vénus au centre du Soleil, en deçà ou au-delà des 4' énoncées précédemment [6]. La différence de durée entre ces éclipses sera inférieure à 17 minutes si Vénus a une latitude plus australe ; mais elle sera plus grande si, les nœuds avançant, elle traverse le Soleil au nord de son centre.
Voici qui réjouira les observateurs passionnés des étoiles, mais qui n’ont pas encore une théorie complète des parallaxes et je tiens à exposer cela davantage, à l’aide d’un schéma et d’un calcul un peu plus minutieux.
Supposons par conséquent que, le 25 mai 1761, à 17h55, à Londres [7], le Soleil occupe 15°37' des Gémeaux [8] et que par rapport à son centre, l’écliptique fasse un angle au Nord de 6°10' [9] ; que Vénus, visible à l’intérieur du disque du Soleil, infléchisse sa trajectoire vers le Sud en faisant un angle de 8°28' avec l’écliptique [10] : alors la trajectoire de Vénus tendra un peu vers le Sud par rapport à l’équateur, coupant les parallèles de déclinaison avec un angle de 2°18' [11]. Supposons même que Vénus se trouve toute proche du centre du Soleil au moment indiqué et qu’elle en soit distante de 4' vers le Sud [12] ; supposons aussi que, chaque heure, elle dessine un arc de 4' à l’intérieur du Soleil, en un mouvement rétrograde [13]. Le demi-diamètre du Soleil sera presque exactement de 15' 51" et celui de Vénus de 37" 1/2. Et supposons, à titre d’essai, que la différence des parallaxes horizontales de Vénus et du Soleil, que nous recherchons, soit de 31", comme il découle de l’hypothèse d’une parallaxe du Soleil à 12" 1/2. Soit donc (Fig.) un petit cercle AEBD de centre C, dont le rayon vaut 31", représentant le disque de la Terre, et sur ce cercle les ellipses des parallèles de 22° et 56° de latitude Nord, dessinées, conformément à l’usage actuel des astronomes pour construire les éclipses de Soleil, avec les points DabE, cde [14] : soit BCA le méridien sur lequel se trouve le Soleil ; sur celui-ci, qu'on incline la droite FHG, représentant la trajectoire de Vénus, avec un angle de 2°18' ; elle doit être distante du centre C de 240 des parties dont BC vaut 31 [15] ; et qu'on abaisse de C la droite CH perpendiculaire à FG. Soit la planète située en H à 17h 55, i.e. à 5h 55 du matin ; qu'on divise la droite FHG en intervalles correspondant aux heures : III-IV, IV-V, V-VI, etc. égaux à CH lui-même, à savoir 4' [16]. Soit également le segment KL, égal à la différence des demi-diamètres apparents du Soleil et de Vénus, soit 15' 13" 1/2. Le cercle de rayon KL étant tracé, ayant pour centre un point quelconque à l’intérieur du petit cercle figurant le disque de la Terre, il coupera la droite FG au point indiquant à quelle heure, à Londres, Vénus, vue de l’endroit du globe terrestre qui se trouve sous le point choisi sur le disque, touchera intérieurement le limbe du Soleil. Et si on trace un cercle de centre C et de rayon KL qui coupe la droite FG aux points F et G, on aura exactement FH = HG = 14' 41" [17], c’est-à-dire la distance que semble parcourir Vénus en 3 heures 40 minutes [18]. F tombera par conséquent en II h 15, à Londres, et G en IX h 35 du matin [19]. D’où il ressort clairement que si la grandeur de la Terre, en raison de cette distance immense, se résumait pour ainsi dire en un point ; ou si, dépourvue de sa rotation quotidienne, elle avait toujours le Soleil à la verticale en un même point C, la durée intégrale de ce passage serait de sept heures un tiers [20]. Mais la Terre étant emportée pendant ce temps par un mouvement opposé à celui de Vénus de 110° de longitude, et la durée s’en trouvant donc réduite, supposons de 12 minutes, il en résultera une valeur très proche de 7h 08 min, soit 107°.
C'est alors au méridien situé sur la rive orientale de l’embouchure du Gange, où la latitude est d’environ 22°, que Vénus sera la plus proche du centre du Soleil. Ce lieu sera donc à égale distance du Soleil, de part et d’autre, au moment de l’entrée et au moment de la sortie de la planète, à savoir 53° 1/2 [=107°/2] puisque les points a et b se trouvent sur le grand parallèle DabE. Le diamètre AB sera, lui, à la distance ab comme le produit des sinus de 53° 1/2 et 68°, c'est-à-dire comme 1'02" est à 46"13"' [21]. Et si l’on fait correctement le calcul (qu’il vaut mieux omettre pour ne pas ennuyer le lecteur), je trouve que le cercle de centre a et de rayon KL coupera la droite FH au point M à II h 20 min 40s ; de même, le cercle de centre b coupera la droite HG en N à IX h 29 min 22s (heure à Londres, bien entendu) [22] ; d’où il ressort que la totalité de Vénus sera visible à l’intérieur du Soleil depuis les rives du Gange pendant une durée de 7h 08 min 42s. Nous avions donc formulé une hypothèse correcte en avançant une durée de 7h 08 min, du fait que la fraction de minute n’a aucune incidence ici.
Si l’on adapte ce calcul à Port-Nelson, je trouve que c’est juste avant le coucher du Soleil que Vénus commencera son passage à travers le disque ; et qu’à l’inverse, elle en sortira juste après le lever du Soleil ; ce lieu se déplace entre temps de c à d en passant par l’hémisphère qui n’est pas éclairé par le Soleil [23], le mouvement de rotation de la Terre se combinant à celui de Vénus. C’est pourquoi la durée du passage de Vénus sera un peu rallongée à cause de la parallaxe, de 4 minutes selon mes calculs ; ce qui fait en tout 7h 24 min, soit 111° de longitude. Et puisque la latitude de ce lieu est de 56°, AB est à cd comme le produit des sinus de 55° 1/2 et 34° c'est-à-dire comme AB = 1'02" est à cd = 28"33"' [24]. Et si le calcul est fait rigoureusement, il apparaîtra que le cercle de centre c et de rayon KL rencontrera la droite FH en O, à II h 12min 45s, et que le cercle de centre d coupera la droite HG en P à IX h 36min 37s [25]. En conséquence, la durée à Port-Nelson sera de 7h 23min 52s, supérieure bien sûr à celle du golfe du Gange de 15 min 10s [26]. Toutefois, si Vénus traverse le disque du Soleil sans latitude [27], la différence en question deviendra de 18 min 40s ; mais si elle passe 4' plus au nord du centre du Soleil, cette différence sera portée à 21 min 40s, et sera bien plus grande encore si la latitude nord de la planète augmente.
À Londres, il découle des hypothèses précédentes que Vénus apparaîtra à un moment où elle aura déjà pénétré à l’intérieur du Soleil et que c’est à 9h 37 du matin que, sortant de cet astre, elle entrera en contact avec son bord intérieur ; et enfin qu’il faudra attendre 9h 56 pour qu’elle soit entièrement sortie du disque solaire. [28]
Il ressort des mêmes hypothèses que Vénus doit toucher de son centre la bordure nord du Soleil le 23 mai 1769 à 11h 00 [29] dans des conditions telles que, en raison de la parallaxe, dans les régions du nord de la Norvège, elle pourra apparaître tout entière à l’intérieur du Soleil qui là-bas ne se couche pas ; tandis que, sur les côtes du Pérou et du Chili, c’est à peine si on la verra entamer, par une fine parcelle de son propre disque, celui du Soleil se couchant à l’horizon ; de même aux îles Moluques et dans leur voisinage, au moment du lever du Soleil. Et si on découvre que les nœuds de Vénus reculent (on peut le soupçonner d'après certaines observations récentes), alors, visible tout entière à l’intérieur du disque solaire, elle offrira une méthode de calcul de la parallaxe du Soleil bien plus précise que jusqu’à présent, grâce à l’écart maximal entre les durées des passages.
A partir des observations menées quelque part dans les Indes Orientales en 1761 sur l’entrée et la sortie de Vénus, et de leur confrontation avec la sortie de l’éclipse visible chez nous, il sera possible de calculer cette même parallaxe en disposant les angles du triangle donné par cette configuration sur les arcs de trois cercles égaux, comme ce sera démontré ultérieurement [30].
Fin
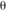 entre l'écliptique et le petit cercle parallèle à l'équateur passant par le Soleil ; sin
entre l'écliptique et le petit cercle parallèle à l'équateur passant par le Soleil ; sin 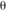 = sin
= sin  .cos
.cos  o où
o où  o est l'ascension droite du Soleil, et
o est l'ascension droite du Soleil, et  est l'obliquité de l'écliptique (
est l'obliquité de l'écliptique ( = 23,471° en 1761).
= 23,471° en 1761). de la trajectoire apparente de Vénus donné par tan
de la trajectoire apparente de Vénus donné par tan  .(
.( LV-
LV- LT) = tan i.(
LT) = tan i.( LV) où i = 3,392°, inclinaison de l'orbite de Vénus sur l'écliptique,
LV) où i = 3,392°, inclinaison de l'orbite de Vénus sur l'écliptique,  LV = 0,06608 °/h et
LV = 0,06608 °/h et  LT = 0,03983 °/h, variations horaires des longitudes héliocentriques de Vénus et de la Terre au moment de la conjonction ;
LT = 0,03983 °/h, variations horaires des longitudes héliocentriques de Vénus et de la Terre au moment de la conjonction ;  = 8,468° = 8°28'.
= 8,468° = 8°28'. -
- 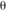 = 2°18' ; en réalité, c'est
= 2°18' ; en réalité, c'est  +
+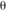 = 14°38'. Cette erreur est décelée dès 1757.
= 14°38'. Cette erreur est décelée dès 1757.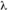 , le point a décrit l'arc ab en suivant le parallèle géographique de latitude
, le point a décrit l'arc ab en suivant le parallèle géographique de latitude  ; la corde ab a pour longueur 2R.sin(90°-
; la corde ab a pour longueur 2R.sin(90°- ).sin(
).sin(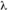 /2) où 2R vaut 2 fois 31" (ou 1'02"). Avec
/2) où 2R vaut 2 fois 31" (ou 1'02"). Avec 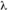 = 107° et
= 107° et  = 22°, on trouve ab = 46"13"'.
= 22°, on trouve ab = 46"13"'.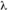 = 111° et
= 111° et  = 56°, on trouve cd = 28"34"' (Halley écrit 33"').
= 56°, on trouve cd = 28"34"' (Halley écrit 33"').