Fiche
pédagogique n°31a
Analyse des observations des contacts
Calcul direct en ligne en temps réel :
P. Rocher, J.-E. Arlot, 3 octobre 2004.
Comment pouvons nous calculer la valeur de l’UA ?
Avant de décrire les méthodes utilisées il convient de bien rappeler la nature de la mesure.
Bien décrire l’expérience.
Nous avons reçu un certain nombre de messages électroniques qui nous laissent à penser qu’une grande partie des participants n’ont pas bien compris le problème et l’assimilent à la mesure de la longueur d’une planche avec une même règle et ils pensent ainsi que l’on fait une série de mesures et que chaque mesure est équivalente à l’autre et qu’il suffit de faire la moyenne de ces mesures, tout le monde ayant mesuré la même chose avec le même instrument. Ce n’est pas du tout cela.
La mesure de l’unité astronomique (ua) n’est pas, en fait, une mesure de distance mais une mesure de temps, et pas du même temps pour tous les observateurs ! En effet, le phénomène observable et mesurable provient de l’effet de la parallaxe diurne de la direction du contact entre le centre de la Terre (que l’on calcule) et le lieu d’observation au moment des contacts. Le temps observé va servir à calculer une ua correspondante.
De plus dans notre expérience nous ne choisissons pas les
parallaxes que l’on mesure, les observateurs ne se déplacent pas (comme aux
siècles passés) vers les lieux optimum d’observation (plus grandes parallaxes)
et leur répartition sur le globe terrestre est aléatoire (en fait biaisée par
l’excès d’inscription en Europe).
Ainsi, pour un calcul en direct de l’unité astronomique, au fur et à mesure de l’arrivée des observations, il n’est pas possible d’appliquer une méthode du type « Delisle » reposant sur l’association de lieux éloignés car on est dans l’incapacité d’associer des mesures de sites différents, n’étant pas maîtres des sites d’observation. Nous sommes donc dans l’obligation de calculer l’unité astronomique par comparaison de chaque observation avec la valeur théorique calculée : quelle doit être la valeur de l’ua pour que la différence entre les instants de contact observé et calculé soient le plus petit possible ? Alors se pose le problème de la convergence de l’algorithme : un Soleil trouvé à l’infini empêchera toute convergence de l’algorithme et interdira de fournir une valeur moyenne pour l’ua. Comme, de plus, nous ignorons à l’avance la dispersion des observations, nous ne pouvons dire si telle observation doit être conservée ou rejetée : il ne faudrait pas que l’algorithme rejette toutes les observations ! Toutes ces considérations montrent que des contraintes fortes doivent être imposées à notre algorithme de calcul en temps réel.
L’algorithme de calcul va donc fonctionner ainsi :
- réception d’une observation de contact, calcul d’une ua
- réception d’une deuxième observation, calcul de l’ua correspondante puis moyenne avec l’ua calculée précédente
- et ainsi de suite, la nième observation reçue fournit une ua calculée qui sera moyennée avec les n-1 ua précédentes calculées.
Notons qu’il n’est pas possible de modifier les critères d’acceptation des observation en cours de journée donc toutes les observations doivent être acceptées et les mauvaises observations ne doivent pas trop perturber le calcul.
Que mesure t’on et que calcule t’on ?
Le problème que l’on résout est le calcul de la parallaxe diurne d’un point de contact au lieu d’observation en mesurant les écarts des temps des contacts entre la valeur prédite du contact et la valeur observée du contact.
La figure ci-dessous permet de comprendre la géométrie du problème.
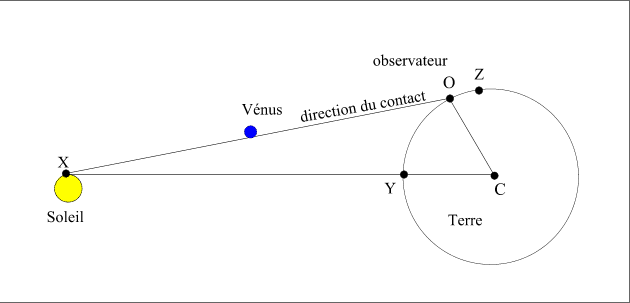
Figure 1 : La parallaxe diurne
Sur cette figure, O est l’observateur, OX est la ligne de visée de la direction du contact et la ligne XC joint le point de contact X sur le bord du Soleil au centre C de la Terre.
Les prédictions sont faites avec la valeur de parallaxe solaire p0=8,794142", donc avec la valeur de l’unité astronomique actuelle parfaitement connue, ua = 149597870 km. La prédiction tc du contact revient à trouver, connaissant la taille du triangle XOC grâce à la connaissance de l’ua, à quel instant a lieu le contact. Mathématiquement on a une relation R (une fonction) qui, pour un lieu quelconque, nous donne une valeur de tc à partir de la valeur ua. Cette fonction dépend de nombreux paramètres physiques que l’on suppose bien connu : diamètre du Soleil et de Vénus en kilomètres, position de l’observateur, rayon équatorial de la Terre, l’aplatissement de l’ellipsoïde terrestre et les positions géocentriques apparentes des centres des deux corps à chaque instant).
Le calcul de l’unité astronomique à partir de l’observation est l’opération inverse (en mathématique la fonction réciproque R-1) : quelle valeur faut-il donner à l’unité astronomique exprimée en kilomètres pour que le temps de contact calculé tc (à l’aide de la relation R) soit le même que la valeur observée ?
On peut donc en théorie, pour chaque observation de contact que vous avez envoyée calculer une valeur de l’unité astronomique correspondante.
Que fait-on avec ces valeurs de l’unité astronomique calculées individuellement ?
La seule chose que l’on puisse faire en temps réel au fur et à mesure que
les observations arrivent, c’est la moyenne des valeurs calculées avec chaque
observation, puis calculer un paramètre statistique qui s’appelle l’écart type
expérimental.
Ici, il faut bien faire la différence entre la mesure que l’on fait, c’est-à-dire la mesure d’un instant et le calcul de l’unité astronomique qui lui est attachée. Ce n’est pas une mesure directe de l’unité astronomique (comme si on avait mesuré une planche avec un double décimètre) mais le résultat d’un calcul : les observations permettent la mesure d’un temps et non pas d’une distance.
Une explication supplémentaire très importante pour la
suite :
Qu’est-ce qu’une bonne mesure ?
Intuitivement nous dirons qu’une bonne mesure est une mesure aussi proche possible de la réalité et qui, par exemple, n’envoie pas le Soleil à l’infini. L’expérience des siècles passés montre qu’une erreur d’une minute peut être très courante parmi les observateurs. Cependant, dans les conditions du XXIème siècle (usage du GPS, enregistrement d’images CCD, utilisation de bonnes optiques, inexpérience des observateurs, …) les choses ont changé mais avant le 8 juin, nous n’avons pas connaissance de ce que sera l’erreur moyenne de mesure, ce qui est très gênant pour le calcul en temps réel.
Par ailleurs, en supposant que nous obtenons des « bonnes » mesures, proches de la valeur réelle, peut-on dire qu’une bonne mesure de l’instant d’un contact donnera une bonne valeur de l’unité astronomique ?
La réponse est : pas toujours, car ça dépend du contact et ça dépend du lieu d’observation.
Il y a deux façons d’expliquer ce phénomène :
· Premièrement, à partir de considérations géométriques : sur le dessin de la figure 1 on voit bien que la forme du triangle XOC dépend de la position de l’observateur O. Si l’observateur est en Y, l’angle OXC est nul, le triangle est complètement aplati et l’on ne peut faire aucune mesure (la parallaxe diurne est nulle et le calcul est indépendant de la valeur de l’unité astronomique), par contre si l’observateur est en Z, l’angle OXC est maximal (l’angle XOC vaut 90°), la parallaxe diurne est maximale. Attention, on ne mesure pas la parallaxe diurne, mais l’effet de la parallaxe diurne sur le calcul des temps de contacts. La forme du triangle caractérise la géométrie du problème, par contre l’effet de la parallaxe diurne peut être nul même si la parallaxe diurne est maximale. Ainsi pour un contact géocentrique donné, tous les lieux sur la Terre définis par l’intersection du cône d’ombre (ou de pénombre, suivant le contact considéré) avec l’ellipsoïde terrestre verront le contact en même temps qu’un observateur qui serait situé au centre de la Terre. Donc plus on s’approche de ces lieux plus l’effet de la parallaxe diurne sera petit.
Un bon lieu d’observation doit vérifier deux critères : avoir une parallaxe diurne la plus grande possible et être le plus loin possible de l’intersection du cône d’ombre (ou de pénombre) avec l’ellipsoïde terrestre. Le plus mauvais lieu d’observation sur Terre, pour cette méthode, est le point de la ligne d’intersection du cône d’ombre (ou de pénombre) qui a une parallaxe diurne nulle donc avec une direction du point de contact au zénith. Pour chaque contact, il n’existe qu’un seul lieu qui réponde à ce critère. En conclusion un bon lieu d’observation doit être loin de cette intersection et doit observer le contact avec un contact bas sur l’horizon.
- Deuxièmement : à partir de la formule linéaire approchée qui nous donne la variation de la parallaxe à partir de la variation de l’écart de temps (voyez la fiche pédagogique n°4b).
![]()
Pour chaque contact les coefficients A, B, C et la valeur dD/dt sont fixes.
Par exemple pour le premier contact intérieur on a :
A = 2,1970, B = 0,2237, C
= 1,1206, dD/dt = –2,9394"/min.
Si l’on nomme ![]()
La variation de la parallaxe pour un écart (to-tc) donné est le quotient de 2,9394 par X, or ce coefficient est fonction des coordonnées de l’observateur, il tend vers zéro lorsque l’observateur s’approche des points du globe dont les coordonnées géographiques sont solution de l’équation X=0.
Ainsi pour un même écart d’observation en temps, on peut obtenir des différences très importantes sur la variation de la parallaxe et donc de l’ua. Celle-ci devient même infinie lorsque X est nul, même avec une très bonne observation !
On peut également signaler la différence géométrique entre le calcul direct et le calcul linéarisé. L’équation X=0 a pour solution l’intersection d’un plan passant par le centre de la Terre avec l’ellipsoïde terrestre, la solution réelle est l’intersection d’un cône avec l’ellipsoïde terrestre, la linéarisation revient donc à remplacer le cône par un plan tangent au cône passant par le centre de la Terre.
Résolution d’un système « contraint ».
Nous avons dit dans nos explications précédentes que l’on pouvait théoriquement calculer la valeur de l’ua pour n’importe quel lieu et n’importe quelle valeur to de contact observée, puis nous avons vu que pour certains lieux ce calcul était impossible et il en est de même pour certaines valeurs de to, car alors, compte tenu de l’hypothèse que nous avons faite sur la valeur de l’ua initiale, la valeur de l’ua calculée devenait infinie. En fait, pour des écarts de temps un peu grands (de l’ordre de plusieurs minutes, ce qui aurait pu être très répandu parmi les observations reçues) le calcul de la fonction réciproque ne converge plus.
Or nous voulions tenir compte de toutes les observations pour faire nos moyennes au fur et à mesure que les observations arrivaient. Pour cela nous avons résolu un système légèrement différent dans lequel on a empêché (contraint) la valeur de l’ua calculée de devenir infinie.
Nous ne pouvions pas contraindre totalement le système car cela reviendrait à fixer la valeur de l’ua. Mais nous pouvions forcer le triangle XOC à garder une dimension finie (c’est-à-dire empêcher le Soleil et Vénus de partir à l’infini). Pour cela dans le calcul de la fonction réciproque, celle qui donne l’ua en fonction du temps observé on a multiplié les vecteurs centre de la Terre-Vénus et centre de la Terre-Soleil par le rapport uac/ua, où uac est l’unité astronomique calculée et ua l’unité astronomique estimée. Ce système, qui converge également vers une valeur de l’ua, a l’avantage d’avoir une solution pour toutes les valeurs possibles des instants de contact permises à la saisie (jusqu’à 30 minutes d’erreur…) mais à condition que l’observateur n’observe pas le contact au zénith. Dans ce dernier cas, le résultat est aberrant quoiqu’il arrive mais le risque est très limité.
Normalement si les observations sont réalistes, c’est à dire si les observateurs envoient réellement les valeurs qu’ils ont observées la moyenne d’un système « contraint » doit être la même que la moyenne d’un système « non contraint » dans lequel on aurait filtré toutes les mauvaises observations. Ce résultat n’est plus vrai si les observateurs rentrent trop de valeurs non réalistes, c’est-à-dire si ils s’amusent à entrer des valeurs aberrantes pour faire des tests numériques. C’est ce qui c’est passé sur notre base après le 18 juin. La base n’étant pas fermée, des personnes entraient des valeurs aberrantes pour voir ce que cela faisait. Ces valeurs aberrantes donnent quand même des valeurs de la parallaxe non aberrantes car le système est contraint, mais cela dégrade la moyenne générale.
Quels effets a l’usage du système contraint ? Pour simplifier nous dirons que les très mauvaises observations deviennent médiocres, que les observations médiocres deviennent bonnes et que les bonnes observations deviennent excellentes. Ainsi par exemple pour Paris des variations de quelques secondes de temps génèrent des écarts que de quelques millièmes de seconde de degré sur la parallaxe et il faut atteindre la minute pour avoir des écarts de l’ordre de deux centièmes de secondes de degré. La méthode sans contrainte donnant, toujours pour Paris, un écart de 2 centièmes de seconde de degré sur la parallaxe pour un écart d’une seconde temps. Même dans la méthode contrainte le lieu d’observation et le contact gardent leur importance, l’effet est différent pour chaque lieu et pour chaque contact. On ne peut donc pas faire de comparaisons numériques entre des lieux et des contacts différents que le système soit contraint ou non.
En conclusion, nous avons donc affiché en temps réel des résultats individuels paraissant très bon dans l’absolu sur la valeur individuelle de l’ua calculée (mais les erreurs individuelles étaient comparables entre elles, d’un observateur à l’autre), alors que la valeur moyenne des résultats était réaliste. En fait un résultat individuel plus réaliste que l’on aurait pu afficher était l’écart entre l’instant mesuré et l’instant prédit. Mais comme l’on a laissé la possibilité de modifier les résultats observés, cela aurait été une très forte incitation à la triche !
Nous avons donné sous forme de graphe l’évolution de la moyenne des valeurs de l’unité astronomique au fur et à mesure que les temps de contact nous étaient fournis, ainsi que la valeur de l’écart type expérimental s. La courbe représentant l’évolution de la valeur de l’ua est obtenue en faisant la moyenne des quatre valeurs de l’ua obtenues pour chaque contact. Ces courbes ont été réalistes jusqu’au 18 juin date à laquelle nous avons commencé à recevoir des résultats aberrants.
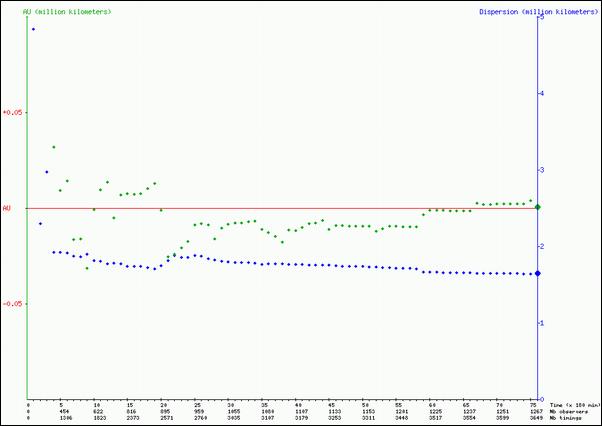
Évolution de la moyenne et de l’écart type expérimental jusqu’au 18 juin.
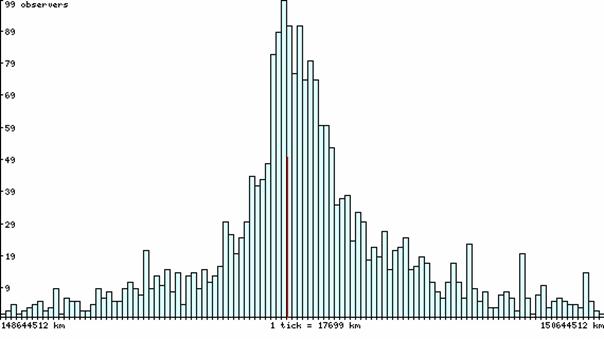
Répartition des valeurs de l’ua calculées avec toute la base.
Voici les résultats obtenus avec le système contraint et tenant compte de toutes les observations (même les plus mauvaises provenant d’erreurs de saisie –cependant limitées à 30 minutes-) :
|
Contact |
Nombre observations |
Moyenne
expérimentale des ua |
Écart à l’ua vraie |
Écart-type
expérimental |
Parallaxe |
|
T1 |
722 |
149908018 |
-310148 |
2062405 |
8,775936" |
|
T2 |
1139 |
149076728 |
521142 |
4878994 |
8,824890" |
|
T3 |
1336 |
149438938 |
158932 |
1409362 |
8,803500" |
|
T4 |
1170 |
149840793 |
-242923 |
4620163 |
8,779890" |
|
Tous |
4367 |
149529684 |
68186 |
3638485 |
8,798158" |
|
Moyenne (T1+T2+T3+T4)/4 |
|
149566119 |
31751 |
|
8,796015" |
Tableau 1
La répartition des valeurs de l’ua calculées avec toute la base nous montre que l’on a pratiquement une répartition gaussienne. La courbe est encore plus belle si l’on supprime les valeurs aberrantes. On peut donc utiliser l’hypothèse d’une loi normale, donc la moyenne des ua calculées est un bon estimateur de l’unité astronomique et l’on peut calculer un écart type sur cette estimateur en divisant l’écart type expérimental par la racine carré du nombre d’observation.
On trouve finalement en utilisant toutes les observations et tous les contacts :
ua = 149 529 684
km +/- 55 059km.
L’écart à la valeur de l’ua « vraie » est de 68 186 km.
Remarquons que dans notre calcul en ligne nous avons publié la moyenne des ua calculées pour chacun des quatre contacts et non la moyenne générale sur toutes les observations. Cela a entraîné un résultat curieux en début d’expérience : en effet un observateur a saisi une valeur du premier ou du deuxième contact pour un contact qui n’avait pas encore eu lieu (le troisième ou le quatrième) ; cela a donné un résultat, unique et faux pour ce contact, qui est entré dans notre moyenne. Par la suite ce mauvais résultat a été moyenné au fur et à mesure que les résultats relatifs à ce contact sont arrivés et son influence a disparue rapidement.
Nous verrons dans la note pédagogique n°31b que le système contraint donne bien des résultats qui sont du même ordre de grandeur que le système non contraint portant uniquement sur les meilleures observations situées dans l’intervalles 16s et 8s autour des valeurs des contacts prédites.