Fiche pédagogique n° 02c :
Tracé des cartes de visibilité du phénomène

P. Rocher (IMCCE)

I. Introduction

Nous avons vu qu’il est possible de calculer les lieux sur Terre correspondant aux premiers et aux derniers contacts de l’ellipsoïde terrestre avec les cônes d’ombre et de pénombre. On peut tracer pour chaque instant de ces contacts les lieux sur Terre qui ont le Soleil (ou Vénus) à l’horizon. Ces lieux sont les intersections avec l’ellipsoïde terrestre du plan normal à la direction Terre-Soleil et passant par le centre de la Terre. Si on néglige l’aplatissement terrestre, ces courbes sont des grands cercles de la sphère terrestre ayant pour pôle la direction du Soleil, ces cercles portent les noms de terminateurs ou de cercles d’illumination. Ces quatre courbes sont les limites de visibilité du phénomène. Elles traduisent le fait qu’à un instant donné pour que le phénomène soit visible, il faut et il suffit que le Soleil et Vénus soient levés.

Nous verrons que pour calculer la parallaxe à l’aide des passages de Vénus devant le Soleil, on a utilisé par le passé deux méthodes. La méthode de Halley qui consistait à comparer des durées de passages et la méthode de Delisle qui consistait à comparer les instants de contacts identiques. On verra également que la précision relative de la parallaxe ainsi trouvée était proportionnelle aux écarts de durées observées dans le cas de la méthode de Halley ou aux écarts de temps des contacts constatés dans le cas de la méthode de Delisle. Il convient donc de connaître en plus des zones de visibilité du phénomène les régions sur Terre qui présentent le plus d’écart en durée du phénomène ou le plus d’écart entre les instants d’un même contact.

II. Remarques importantes sur l’effet de la parallaxe.

On appelle effet de parallaxe, la différence d’aspect que présente le passage de Vénus selon que l’on observe depuis un lieu à la surface de la Terre ou au centre de la Terre ; où selon que l’on observe le passage en deux lieux distincts à la surface de la Terre.

Vu depuis le centre de la Terre, le trajet de Vénus sur le disque solaire est une corde parcourue pratiquement avec une vitesse constante. Cette vitesse est combinaison des mouvements apparentes des deux astres.

Le fait de ce placer à la surface de la Terre complique cet aspect, car il convient alors de tenir compte du mouvement de rotation de l’observateur à la surface de la Terre. Or cette rotation se fait parallèlement au plan de l’équateur terrestre qui est incliné par rapport à l’orbite apparente du Soleil. Cela va se traduire par un déplacement de la trajectoire de Vénus sur le disque solaire et des décalages horaires pour les différents contacts. La trajectoire de Vénus n’est plus une corde mais une hyperbole et surtout la vitesse de déplacement ne peut plus être considérée comme constante durant le passage. Il convient également de noter que les décalages horaires ne sont pas égaux aux différences de longitude des lieux et que les lignes de début, de fin et de maximum à un instant donné n’ont aucune raison d’être des méridiens terrestres.

II. Interprétation géométrique des formules donnant la parallaxe en coordonnées différentielles planes tangentielles.

Nous avons vu que les parallaxes U et V en coordonnées différentielles planes tangentielles peuvent se mettre sous la forme suivante :

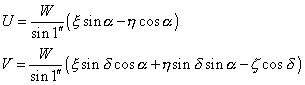
en posant :

et que les coordonnées différentielles topocentriques affectées de l’indice p peuvent s’écrire sous la forme approchée :

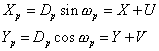
Nous allons donner une interprétation géométrique de ces formules.

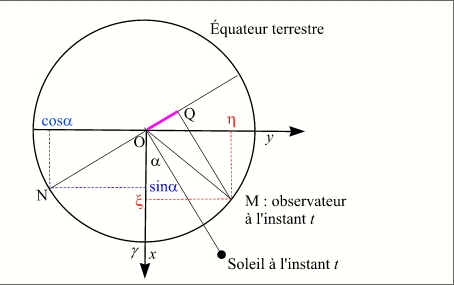
Figure 1. – Interprétation géométrique.

Si l’on néglige l’aplatissement terrestre, on ne commet pas sur U et V d’erreurs supérieures au dixième de seconde.

Soit N le point de l’équateur terrestre (figue 1) dont l’ascension droite est égale à a – p/2; ce point est un des pôles du méridien où se trouve le Soleil à l’instant t, et le rayon ON a pour coordonnées dans le repère équatorial cartésien (sina, -cosa,0).

Si M est la position de l’observateur à l’instant t, la projection OQ de OM sur ON a pour valeur : , le rayon terrestre ON a également pour valeur p₀ sin1".

On a donc :

et, par suite :

De même si on appelle n le point de la sphère terrestre de coordonnées (a,d-p/2) si d>0° ou de coordonnées (a+p, -d-p/2) si d<0°, les coordonnées de On dans le repère équatorial cartésien sont les suivantes : (sind cosa, sind sina, -cosd)

et : est la projection de OM sur On.

On a donc :

et

Les points N et n sont sur le cercle d’illumination correspondant à l’instant t.

L’écart entre la distance topocentrique des centres des astres et la distance géocentrique des mêmes centres s’écrit alors :

Or, si l’on porte à partir du point N, sur le cercle Nn, un arc égal à w-p/2 dans le sens Nn si w<p/2 où dans le sens opposé si w>p/2 , on a :

L’équation précédente s’écrit alors

et

La valeur de W étant positive, on en déduit qu’à l’époque t, D_p sera maximal pour un observateur situé en A, et sera minimal pour un observateur situé au point B, antipode de A, et appartenant comme lui au cercle d’illumination. De plus à l’instant t, D_p aura la même valeur pour tous les points des cercles ayant A et B pour pôles.

Or on a vu que l’expression (4) peut également s’écrire sous la forme (équation 13 de la fiche II) :

avec

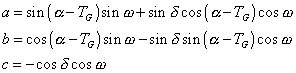
On en a déduit que

On a vu que les coefficients a, b et c sont indépendants de l’observateur, mais varient avec le temps, principalement à cause des changements rapides que subissent les angles T_G et w durant le passage. En remarquant de nouveau que l’on a la relation suivante :

si l’on détermine la longitude l_D et la latitude j_D vérifiant les relations suivantes :

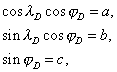
donc le point sur la Terre qui a comme coordonnées cette latitude et cette longitude est précisément le point A pour lequel D_p est maximal à l’époque t. De même le point B situé à l’antipode de A, donc de coordonnées l_D + 180° et -j_D , est le point pour lequel D_p est minimal à l’époque t.

On en déduit le théorème important suivant : à chaque instant t, la distance apparente entre les centres des deux astres est la même pour tous les points de la surface de la Terre pour lesquels à la même valeur, c’est-à-dire pour tous les lieux situés sur des petits cercles ayant pour pôle le point A et pour distance polaire la valeur .

Utilisation des distances entre les centres des deux astres.

Si l’on veut calculer la parallaxe solaire en mesurant au même instant t, en deux lieux différents, les distances entre le centre de Vénus et le centre du Soleil, on doit déterminer quelles sont les lieux d’observations les plus favorables.

Pour cela on calcule les coordonnées géographiques des points A et B à l’aide des formules précédentes. On trace le cercle d’illumination correspondant à l’instant t considéré. Puis on cherche dans la zone éclairée quelles sont les lieux d’observations possibles aux voisinages des points A et B et l’on calcule pour ces lieux les valeurs D_p à l’aide de la formule (6). On conserve les combinaisons pour lesquelles les valeurs de D_p diffèrent le plus. Cette recherche est répétée sur toute la durée du passage, avec un pas constant, d’heure en heure par exemple. Il convient de remarquer que les observations de distances faites vers le milieu du passage, c’est-à-dire lorsque D est proche de son minimum, offrent un avantage particulier. En effet, les mesures que l’on aura à comparer ne se rapporteront pas exactement au même instant, et l’on devra réduire l’une au temps de l’autre ; or cette réduction sera simple si D varie le moins possible, donc près du minimum de distance.

Utilisation des instants des contacts.

Si l’on utilise l’indice i (i = 1 et 2) pour les premiers contacts, l’écart de temps entre les contacts topocentriques T_i et les contacts géocentriques t_i identiques, pour un point M quelconque de la surface terrestre est donnée par  :

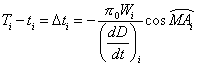
ou

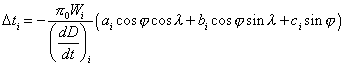
Au moment des premiers contacts, la distance D entre les centres des astres diminue, sa dérivée par rapport au temps est donc négative. Les contacts les plus tardifs correspondent donc au voisinage des points A_i et les contacts les plus hâtifs correspondent au voisinage des points B_i situés aux antipodes des points A_i.

On peut faire un raisonnement identique pour les derniers contacts topocentriques et l’on aura la formule suivante :

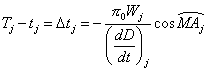
ou

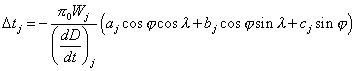
l’indice j (j = 3 et 4) correspondant aux derniers contacts.

Dans le cas des derniers contacts, la distance D entre les centres des astres augmente, sa dérivée par rapport au temps est donc positive. Les sorties les plus hâtives ont donc lieu aux points A_j et les sorties les plus tardives aux points B_j, aux antipodes des points A_j.

On remarquera que tous les points A_i, A_j, B_i et B_j se trouvent sur les courbes limites de visibilités du passage et correspondent toujours à un Soleil à l’horizon donc à des contacts au lever ou au coucher du Soleil.

La connaissance des points A_i, A_j, B_i et B_j nous permet de tracer les courbes représentant les lieux sur Terre où les contacts topocentriques, c’est-à-dire les entrées et les sorties de Vénus sur le disque solaire, ont lieu à un instant donné. Ces courbes sont les cercles de la sphère terrestre ayant les points A_i, A_j, B_i et B_j pour pôles, la distance polaire à ces points se calculant simplement en inversant les formules précédentes.

La connaissance de ces courbes est particulièrement intéressante car elle permet de choisir judicieusement les lieux d’observations lorsque l’on désire utiliser la méthode de Delisle.

Utilisation des durées des passages

Si les écarts entre les instants des contacts géocentriques (t_j,t_i) et topocentriques (T_j,T_i) sont donnés par les formules (9) et (11), la durée DT_p du passage topocentrique s’écrit en fonction de la durée du passage géocentrique DT sous la forme :

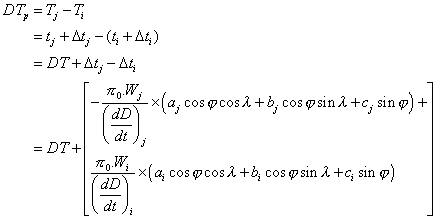
et en posant :

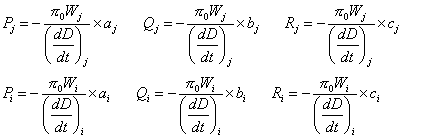
la formule précédente s’écrit :

et si l’on détermine le nombre g positif et la latitude j_g et la longitude l_g tels que :

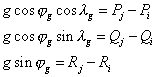
et si l’on nomme C le point de la sphère terrestre ayant ces coordonnées, alors l’expression précédente devient :

(13)

On peut de nouveau reprendre les raisonnements précédents, le point C est le lieu où le passage topocentrique est le plus long et son antipode D est le point où la durée du passage est la plus courte. Les cercles de la sphère terrestre ayant pour pôles ces deux points correspondent aux lieux présentant la même durée du passage. Contrairement aux points A et B, un seul des points C et D se trouve dans la partie de visibilité du passage.

Les courbes d’égale durée, limitées aux zones de visibilité complète du passage, sont particulièrement utiles si l’on désire trouver des lieux d’observations optimisés pour l’application de la méthode de Halley.