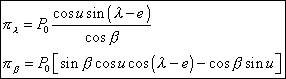Fiche pédagogique n° 04a :
Formulation de la
parallaxe dans les différents repères astronomiques
P. Rocher (IMCCE)
I. Introduction
Cette fiche contient les différentes formes que prend la parallaxe en
fonction des repères célestes dans lesquels elle est exprimée. En astronomie on
utilise trois repères principaux : le repère horizontal local construit à
partir du plan horizontal et du zénith, le repère équatorial construit à partir
du plan équatorial et du pôle céleste et le repère écliptique construit à
partir de l’écliptique (plan orbital de la Terre) et de la normale à ce plan
(pôle de l’écliptique). La formulation de la parallaxe devient de plus en plus
complexe au fur et à mesure que l’on passe du premier au dernier repère. Pour
comprendre et pouvoir utiliser la parallaxe dans les calculs des passages de
Vénus devant le Soleil, l’on doit au minimum utiliser les deux premières
formulations. L’élaboration de ces formules fait appel aux formules de la
trigonométrie plane et sphérique.
II. La parallaxe horizontale
La parallaxe horizontale est exprimée dans le repère sphérique local défini par l’horizon et le zénith d’un lieu d’observation. Les variables angulaires de ce repère sont la hauteur h au dessus de l’horizon et l’azimut a angle entre la projection horizontale du corps et la direction du sud. On utilise également le complémentaire de la hauteur, compté à partir du zénith, cet angle z porte le nom de distance zénithale. C’est dans ce repère que la parallaxe a sa formulation la plus simple.
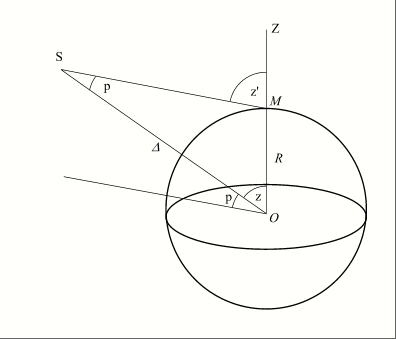
Figure 1. – La parallaxe horizontale.
Soient O le centre de la Terre, M un observateur, Z la direction du zénith pour l’observateur M.
Soit S un corps du système solaire, D est la distance entre ce corps et le centre de la Terre et R est le rayon terrestre (figure 1).
La distance zénithale z' de l’astre vue depuis M est la distance zénithale apparente et la distance zénithale z vue depuis le centre O de la Terre est la distance zénithale vraie.
L’angle z'-z = p est la parallaxe en distance zénithale ou en hauteur de l’astre. La parallaxe agit en sens inverse de la réfraction atmosphérique. Elle diminue la hauteur de l’astre et augmente sa distance zénithale.
On a ![]()
La parallaxe horizontale P0 est la valeur de la parallaxe prise pour un astre à l’horizon en M, dont pour z' = 90°.
![]()
La parallaxe zénithale peut donc s’écrire :
![]()
Et si les angles sont petits : ![]()
Lorsque la parallaxe est faible on peut confondre le sinus avec l’angle exprimé en radians, on peut donc exprimer P0 en secondes de degré à l’aide de la formule suivante, sin1" permet de transformer les radians en secondes de degré :
![]()
La parallaxe équatoriale solaire moyenne.
On la note p0, c’est la valeur de la parallaxe horizontale solaire lorsque la Terre est située à une unité astronomique (a) du Soleil. Les trois constantes R, a et p0 sont reliées par la relation (2) la connaissance de deux de ces valeurs contraint la valeur de la troisième. Il convient donc dans les calculs de prédictions d’utiliser des valeurs cohérentes de ces paramètres.
Ainsi les constances UAI 1976 et de l’IERS 1992 sont les suivantes :
UAI 1976 IERS
1992
R = 6 378.140 km R = 6 378.1363 km
a = 149 597 870 km a =149 597
870.61 km
p0 = 8.794148" p0 = 8.794142"
III. Les parallaxes équatoriales
Si l’on se place dans le repère équatorial local il convient d’exprimer la parallaxe en ascension droite et la parallaxe en déclinaison.
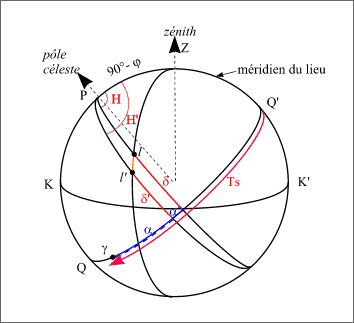
Figure 2. – La parallaxe dans le repère équatorial.
Soit l la position géocentrique de l’astre, l'
sa position topocentrique, la parallaxe en hauteur p est l’angle ![]() (figure 2).
(figure 2).
Soit a et d les coordonnées équatoriales de l, a' et d' les coordonnées équatoriales de l' et, H et H' les angles horaires respectifs de l et l'.
La parallaxe en angle horaire pH est égale à : H' – H et la parallaxe
en déclinaison pd est
égale à d'- d.
Calcul de la parallaxe en angle horaire et en ascension droite.
Dans le triangle sphérique l'Pl on a la relation :
![]()
Dans le triangle sphérique Pl'Z on a :
![]()
j étant la latitude du lieu.
En combinant ces deux équations on obtient :
![]()
Or on a : ![]() et finalement :
et finalement :
![]()
Et si les angles pH et P0 sont petits :
![]()
Comme H' ~ H, sin H' ~ sin H = sin (T - a), T étant le temps sidéral local de l’observateur
D’où ![]()
La parallaxe en ascension droite pa est l’opposée de la parallaxe en angle horaire, on a donc :
![]()
On peut également faire apparaître dans cette formule les coordonnées cartésiennes équatoriales de l’observateurs (x,h,z) définies par
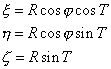
P0 peut se mettre sous la forme R/D et si l'on développe le sinus dans la formule (5) on obtient :
![]()
Calcul de la parallaxe en déclinaison.
On a par définition
![]()
Dans le triangle sphérique PZl on a la relation
![]()
![]()
On a une relation identique dans le triangle sphérique ![]()
![]()
En remplaçant dans la première formule ![]() par sa valeur issue
de la seconde on obtient :
par sa valeur issue
de la seconde on obtient :
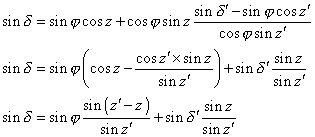
Or z' – z est la parallaxe en distance zénithale donc :
![]()
![]() d’où
d’où ![]()
Or dans les triangles sphériques ZPl et ZPl' on a
![]()
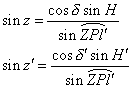
![]() d’où
d’où
![]()
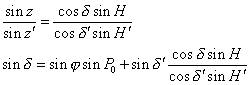
![]() d’où
d’où
![]()
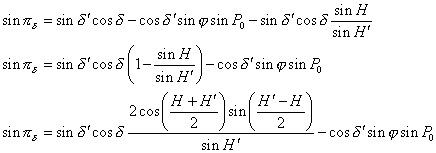
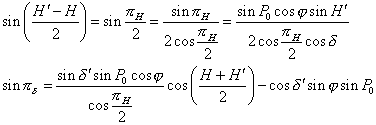
Pour Vénus et le Soleil les parallaxes étant faibles, on peut simplifier en posant dans cette formule :
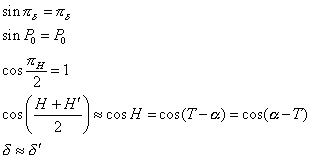
On obtient alors :
![]()
De même on peut faite apparaître dans cette formule les coordonnées cartésiennes équatoriales de l’observateur.
On a alors :
![]()
Remarques : si l’on tient compte de l’aplatissement terrestre, il convient de remplacer dans ces formules sin j et cos j par r sin j' et r cos j'. Où r est la distance géocentrique du lieu et j' sa latitude géocentrique.
Les équations (4) (5) et (7) deviennent :
![]()
![]()
![]()
IV. Les parallaxes écliptiques
Les expressions de la parallaxe en variables écliptiques sont beaucoup plus complexes, elles ne sont plus utilisées de nos jours dans les calculs des passages. Par contre elles ont été utilisées par le passé, car c’est dans ce repère que les théories planétaires de Vénus et de la Terre sont construites.
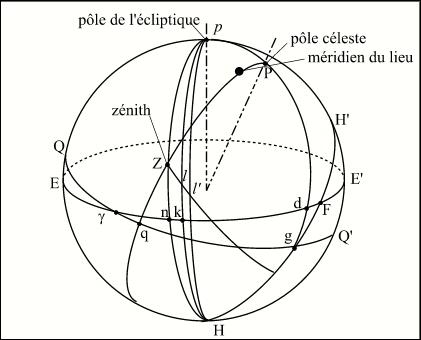
Figure 3. – La parallaxe dans le repère écliptique.
Sur la figure ci-dessus :
P est le pôle céleste, p le pôle de l’écliptique et Z le zénith du lieu.
EE' est le grand cercle de l’écliptique, QQ' est le grand cercle de l’équateur et HH' le grand cercle de l’horizon.
g est la direction de l’équinoxe, origine des longitudes écliptiques et des ascensions droites.
n est la projection du zénith Z sur l’écliptique, ce point se nomme le nonagésime.
Zn = u est la distance zénithale du nonagésime et gn = e sa longitude écliptique.
On remarque également que pZn est normal à l’écliptique et à l’horizon, F intersection de l’écliptique et de l’horizon est le pôle du grand cercle passant par Z et p.
l est la position géocentrique l’astre et l' la position topocentrique de l’astre.
gk = l et gk = b sont la longitude et la latitude du point l.
La parallaxe en longitude pl
est égale à l’angle gpl' - gpl, la parallaxe en latitude pb est
égale à pl' – pl.
On peut utiliser des formules identiques aux précédentes, il suffit de remplacer :
PZ = p/2 - j par pZ = p/2 - Zn
ZPl = H par Zpl = gpl – gpZ = gk –gn
Pl = p/2 - d par pl = p/2 - b
Calcul des coordonnées du nonagésime.
Le grand cercle pPdg a pour pôle l’équinoxe g, donc gd = gg = p/2, l’angle gq est le temps sidéral du lieu (angle horaire du point g).
Dans le triangle sphérique ZPp en remarquant que Zp = p/2 - u et que pP est égale à l’obliquité e.
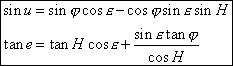
si l’on tient compte de l’aplatissement terrestre ces formules deviennent :
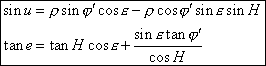
Les parallaxes écliptiques ont alors la forme suivante :