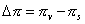 which will allow us to calculate the parallaxes.
which will allow us to calculate the parallaxes.P. Rocher (IMCCE)
In this note we will present a simplified calculation of the average equatorial parallax of the Sun. This simplification of calculation is done at the price of an important constraint for the observations. We will suppose that we have two simultaneous observations which provide us the distance between the two apparent centers of the planet Venus in front of the solar disc. We will indicate the approximations and simplifications which we carry out.
Let be two places of observations M1 and M2, sufficiently distant; two observers note at the same moment T the position of the apparent center of the planet Venus in front of the solar disc. Then using these two observations, it determines the distance which joins these two apparent Venus centers. The measurement of this distance expressed in solar radii, makes it possible to calculate the equatorial mean parallax of the Sun p0. We will see that this measurement is far from being simple.
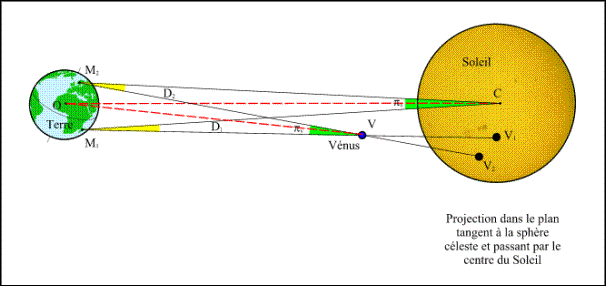
Figure 1. - Observation of the Venus transit from two sites at the same moment
Let O be the center of the Earth, C the center of the Sun, V the Venus center and V1 and V2 the Venus centers on the solar disc seen respectively from the points M1 and M2. Let us note D1 and D 2 the angles CM1V and CM2V formed by the directions of the lines joining the two points of observations to the centers of the Sun and Venus and note p S the angle under which one sees the segment M1M2 from the Sun and pv the angle under which one sees the segment M1M2 from Venus. These two angles are the parallaxes of the Sun and Venus seen from the sites M1 and M2 (figure 1).
If the two points M1 and M2 are unspecified on terrestrial surface in the zone of visibility of the passage, there is no reason for the four points M1, M2, V and C to be in the same plane. Thus the lines M1C and M2V are not in the same plane and do not cut themselves. One cannot thus observe the rules of the geometry in the plane in the figure1.
And the following relation :
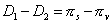
is false. It is true only if the four points are coplanar.
Contrarily, the difference of the parallaxes is equal to the angular distance between the two apparent centers of Venus (figure 2).
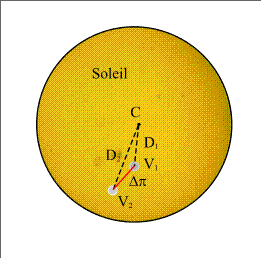
Figure 2. – Apparent positions of Venus on the solar disc.
It is checked that this difference is equal to D2 - D1 when the four points are coplanar i.e. when V1, V2 and C are aligned.
The value that the observers will measure is thus
the distance Dp between
the two apparent centers of Venus and it is the relation
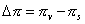 which will allow us to calculate the parallaxes.
which will allow us to calculate the parallaxes.
For that we will express the two parallaxes according to the distances between the center of the Earth and the center of Venus and the Sun. Let be RV the distance between the center of the Sun and the center of Venus and RT the distance between the center of the Earth and the center of the Sun, the distance Venus-Earth is thus equal to RT - RV. To express this parallax we must also know projection D of the distance between the two points M1 M2 on the normal plane to the direction Earth-Sun (figure 3).
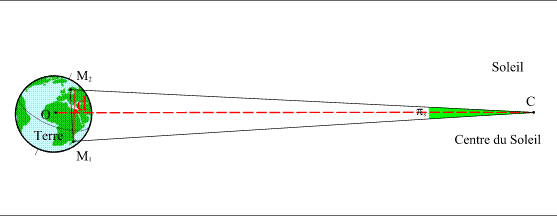
Figure 3. – Solar parallax related to the points M1
et M2.
As the terrestrial radius and the distance between the two points are small compared to the distances Earth-Sun and Earth-Venus, the parallaxes are given by the following approximate formulas :
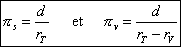 (1)
(1)
Actually, the exact parallax are given by :
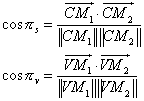
Then we have the following relation :
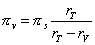 (2)
(2)
and
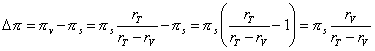
or
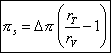 (3)
(3)
The measurement gives us the value Dp expressed in solar diameter and one must also measure the diameter of the Sun, because if the distance Earth-Sun is unknown, this diameter may not be calculated.
To know the solar parallax, it is thus necessary also to know the ratio of the distances Sun-Earth and Sun-Venus. However this ratio can be calculated thanks to the laws of Kepler.
The first law of Kepler says to us that the planets describe elliptic orbits around the Sun and that the Sun occupies one of the focus of these ellipses. At a given moment the radius vector Rp joining the center of the Sun to a planet p is calculated using the following formula :
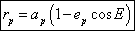 (4)
(4)
Where ap is the equatorial radius of the ellipse, ep is the eccentricity of the ellipse and E is an angle called eccentric anomaly which makes it possible to situate the planet on its orbit.
The third law of Kepler provided a relation between the equatorial radii of the orbits and the periods of revolution of the planets, thus for the same central body all the orbits of the planets which revolve around this central body check the following relation :
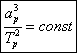 (5)
(5)
The laws of Kepler thus describe the orbits of the solar system except for a scale factor. The observation of the periods of revolution of planets gives us the ratio of the semi-major axis, thus the ratio of the semi-major axis of the orbits of Venus and of the Earth is equal to :
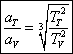 (6)
(6)
and at any date T, the ratio of the radius vectors is equal to
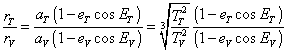 (7)
(7)
Thus the laws of Kepler make it possible to calculate the ratio of the radius vectors for any date T.
Our measurement allows us to calculate the value pS, it is thus appropriate now to pass from this value to the value of the mean equatorial parallax of the Sun p0 .
The mean equatorial parallax of the Sun p0 is by definition the angle under which one sees the equatorial radius of the Earth from the center of the Sun when the Sun is at one astronomical unit from the Earth.
We have thus the following relation :
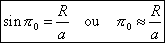 (8)
(8)
R being the terrestrial equatorial radius and a the astronomical unit.
However the equation (1) gives us the value of the solar parallaxpS according to the distance R T Earth-Sun and of projection d of the distance between the points of observations on the normal plane to the direction Earth-Sun.
It is enough to express this distance D in terrestrial radius and the distance Earth-Sun in astronomical unit to have a relation between pS and p0.
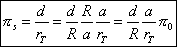 (9)
(9)
It remains only to
calculate the D on R ratio .
The a/RT ratio is
provided to us by the first law of Kepler (cf formulae 4).
However if one makes the vector product of the two vectors
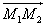 and
and
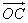 one obtains :
one obtains :
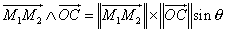 (10)
(10)
However the product of the length of the first vector by the sine
of the angle between the two vectors
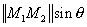 is equal to the distance d. In the same way the length of
is equal to the distance d. In the same way the length of
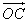 is equal to the distance RT
is equal to the distance RT
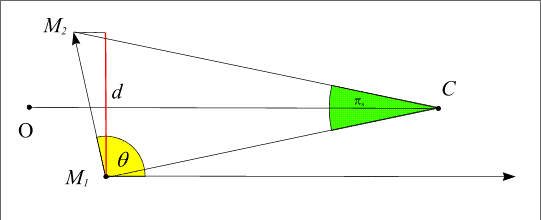
Figure 5. -
Solar parallax related to the points M1
and M2.
The resolution of equation 10 gives us the value of d.
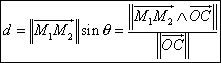 (11)
(11)
Note : if the concept of vector product
is not known, one can use the scalar product of the same vectors, that
allows to calculate the cosine of the angle, then his sine using the
relation : 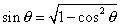 .
.
This calculation on the vectors requires to know the Cartesian co-ordinates of the two points M1 and M2 and of the center of the Sun C in a orthonormed reference frame (O, x, y, z) centered on the center of the Earth. We will use the geocentric apparent equatorial reference frame for this calculation.
This reference frame is defined by the plan of the terrestrial equator at the date T of the observation (plane Oxy) and by the direction of the northern celestial pole of the axis of rotation of Earth (Oz). In this reference frame one can define a Cartesian reference frame (x, y, z) and a polar reference frame (a, d, R) the two angles having the name of right ascension and declination. One passes from one system to the other by the following relations :
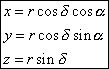 (12)
(12)
and the relations opposite
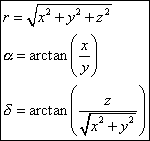 (13)
(13)
The direction of axis Ox at the date T is the direction of the vernal equinox at the same date.
The ephemerides (i.e. the Kepler's laws) provide us the equatorial geocentric coordinates of the center of the Sun (a, d); thedistance is not know but it is not important
because the vector
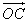 may be replaced by its unit vector in equation 11.
may be replaced by its unit vector in equation 11.
The more complicated problem is the determination of the cartesian coordinates of the points M1 et M2 in this equatorial frame.
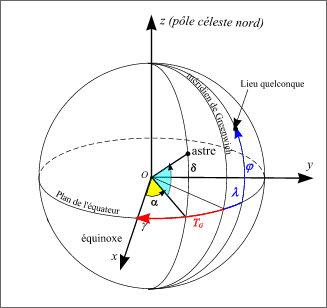
Figure 6. – Geocentric equatorial coordinates.
The position of a point at the surface of the Earth is given by its latitude and its longitude (geographic); the latitude is given referred to the terrestrial equator, so that it is an angle such as the declination. The longitude is given referred to a meridian origin (Greenwich meridian), so that it is an angle similar to the right ascension, but with an origin different from the one of the equatorial lestial coordinates. It is then necessary to know at each date the angle between the direction of Ox axis and the direction of the projection of the meridian origin in the equator plane (cf. figure 6). This angle is related to the rotation of the Earth: it is named the "sidereal time" of the Greenwich meridian and its increases by 360° during 23h 56m 4s (sidereal revolution of the Earth).
So, it is sufficient to know the sidereal time of Greenwich TG at 0h UTC for the day of the transit to know the sidereal time of Greenwich at any time t , then the sidereal time of any point on Earth having a longitude l.
 (14)
(14)
One will pass from the sideral Greenwich time to the sidereal time of the site M having the longitude l, by adding or substracting this longitude.
Attention, sidereal time increases when going towards east
from of the meridian
of Greenwich; it is thus appropriate to pay attention to the convention of sign
well used
to note longitudes.
If the longitudes are counted negatively towards east
then
the relation linking local sidereal time to the meridian line of the site of
longitude l and sidereal time
with the meridianof Greenwich is as follows:
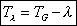 (15)
(15)
Attention les deux angles doivent être exprimés avec la même unité (degrés ou heures).
Alors les coordonnées cartésiennes d’un point M1 de coordonnées géographiques (j1, l1) à l’instant t sont données par :
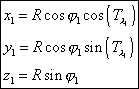 (16)
(16)
The length
 of the vector
of the vector
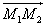 (its modulus) and its coordinates (X, Y, Z) are given by :
(its modulus) and its coordinates (X, Y, Z) are given by :
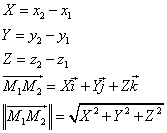 (17)
(17)
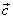 of the direction « center of the Earth - Sun » is given by :
of the direction « center of the Earth - Sun » is given by :
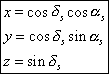
The vector product
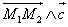 and its modulus are then :
and its modulus are then :
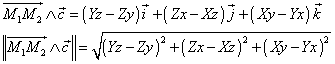 (19)
(19)
and finally, using formula (11), one will get :
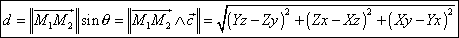 (20)
(20)
And the mean equatorial parallax is given (following (9) by :
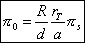 (21)
(21)
We will take as an example the observation made at Antananarivo (Madagascar) and at Helsinki (Finland) at the date t=8h 30min on June 8, 2004.
The geographic coordinates of Antananarivo are :
Latitude :18° 52' south, longitude : 47° 30' east then j1 = –18,866667° and l1 = –47,5°.
The geographic coordinates of Helsinki are :
Latitude :60° 8' north, longitude : 25° 3' east, then j2 = 60,133333° and l2 = –25,05°.
The geocentric equatorial coordinates of the Sun at 8h 30m UTC are provided by the ephemerides :
Right ascension of the Sun as = 76°49' 36.493"
Declination of the Sun ds = +22°53' 16.237"
The sidereal time at bGreenwich at a date t in UTC is provided by the following formula :
TG (t UTC) = 17h 6m 51,31s + 1,002737908 t
Then the sidereal time at Greenwich at 8h 30min is equal to :
TG = 17h 6m
51,31s + 8h 31m 23,78s = 25h 38m 15,09s = 1h 38m 15,09s
It is necessary to convert it in degrees before calculating the local sidereal
time for the two cities.
TG = 1h 38m
15,09s = 24,562875°.
From this, one will deduce the local sidereal time at 8h 30m at Antananarivo :
Tl1 = 24,562875 – (–47,5°) = 72,062875°
And the sidereal local time at 8h 30m at Helsinki is :
Tl2 = 24,562875 – (–25,05°) = 49,612875°
One will deduce from this the cartesian equatorial coordinates for these
two cities :
Antananarivo :
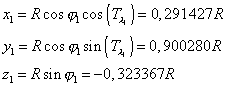
Helsinki :
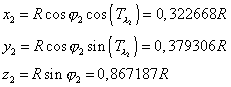
The coordinates of the unit vector  of the direction Earth-Sun are obtained through formula 18 :
of the direction Earth-Sun are obtained through formula 18 :
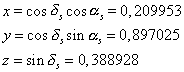
The vector
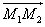 has as coordinates :
has as coordinates :
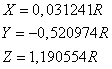
Formula 20 allows us to calculate the value of d :
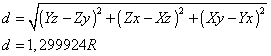
The ephemerides provide us the ratio between the radii vectors and the ratio between the distance Earth-Sun and the semi-major axis of the orbit of the Earth at the given date :

Now, we will just have to make an hypothesis on the measured values, i.e. on Dp and on the solar diameter :
We will suppose that :
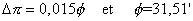
That gives the value of Dp : 28,359"
Formula 3 provides us the value of the solar parallax :
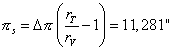
And formula 21 provides us the value of the mean equatorial parallax :
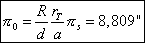
The value that we finds is relatively close to reality, but it depends only on the measure of the distance from the apparent centers of Venus on the solar disc and on the size of the solar diameter. The apparent size of the solar diameter can be measured with a good precision; on the other hand the measurement of the distance between the apparent centers of Venus is not obvious, on a traditional photographic stereotype, the apparent diameter being around 20mm, the distance from the centers is then of 0,3mm and a precision of one thousandth corresponds to a measurement to 0,02mm.
In the preceding forms, one occulted a certain number of difficulties
to simplify the problem. Here the list of the complications which appear if
one wants to make a rigorous calculation:
1. Because of the mutual disturbances, the orbits of the planets do not follow
the laws of Kepler (valid only for two bodies) but more complex trajectories.
2. This is not the Earth which has a quasi-elliptic orbit around the Sun but
the barycentre of the system Earth-Moon.
3. Following the movement of the axis of rotation of the Earth (precession and
nutation), the origine Ox of the equatorial reference frame is not fixed relatively
to time.
4. The light being propagated with a finished speed, the positions of the Sun
and Venus at a given date t are not geometric positions but positions
of two bodies at the date t – tp, tp being the time used by the light to go from each
body and the Earth. Since these distances are not supposed to be known, it is
necessary to iterate the calculations to take it into account.
We saw, in the sheet n°04b, that it exists two simplified formulae allowing to calculate directly the parallax from the comparison of the dates of the same contact seen from two different sites (Delisle method) or from the comparison of the duration of the transit observed from two different sites (Halley method).
We will study simultaneouly these two aspects from the preceeding numerical example.
The mean equatorial solar parallax
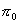 is obtained by comparing
two identical contacts using the following simplified formula
(cf. formula 16 of the sheet n°04b) :
is obtained by comparing
two identical contacts using the following simplified formula
(cf. formula 16 of the sheet n°04b) :
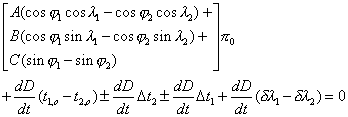
If one neglect the uncertainties and the errors, then, the formula becomes :
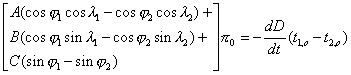
Same, the mean equatorial solar parallax is obtained by comparing the two identical duration, using the following formula (cf. formula 21 of the sheet n°04b) :
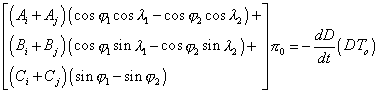
i and j are the index related to the same contacts : i = 1, j = 4 for the external contacts and i = 2, j = 3 for the internal contacts.
The coefficients A, B, C and the
term 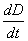 are calculated for
each contact and are given by the following table :
are calculated for
each contact and are given by the following table :
|
Description of the contact |
A |
B |
C |
dD/dt "/min |
|
First external contact (index 1) |
2,2606 |
-0,0194 |
1,0110 |
-3,0846 |
|
First internal contact (index 2) |
2,1970 |
0,2237 |
1,1206 |
-2,9394 |
|
Last internal contact (index 3) |
-1,0929 |
-1,1376 |
1,9090 |
2,9391 |
|
Last external contact (index 4) |
-0,9799 |
-1,3390 |
1,8383 |
3,0842 |
We will take again the example of the same two cities with the observational hypothesis as follows :
City n°1 : Antananarivo (j1 = –18,866667° et l1 = –47,5°)
Date of the first observed internal contact (index
2) : t2 = 5h 35m 30s UTC.
Date of the last observed internal contact (index 3) : t3 = 11h 8m 4s UTC
Observed duration of the transit (internal): 5h 32m 34s.
City n°2 : Helsinki (j2 = 60,133333° et l2 = –25,05°)
Date of the first observed internal contact (index 2) :
t2 = 5h 38m 38s UTC.
Date of the last observed internal contact (index 3) :t3 = 11h 2m 20s UTC
Observed duration of the transit (internal) : 5h 23m 42s.
In the formulae (22) and (23) the factors of the coefficients A, B, C are identical and may be calculated separately:
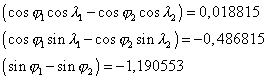
Calculation of the parallax using the first contacts :
The differences between the dates of the first internal contacts
is –3m 8s (–3,1333m), and the use of the values of the coefficients A2,
B2, C2 and 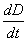 in the formula (22)
will provide us the following equation :
in the formula (22)
will provide us the following equation :
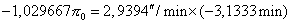
That provides 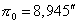 .
.
Calculation of the parallax using the duration of the internal transits
The difference in duration of the internal transits is
8m 52s (8,866m), and the use of the values of the coefficients A2, B2,
C2, A3, B3, C3
and 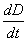 in the formula (23)
provides us the following equation :
in the formula (23)
provides us the following equation :
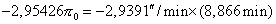
Attention, it is the value 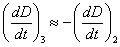 and mainly its sign which may be used.
and mainly its sign which may be used.
That gives 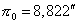 .
.
Let us remind that these methods are not completely accurate and one should use more complete formulae for the reduction of the observations.