Educational sheet
n°05c :
Formulae for the calculation of the solar parallax
from observations of the distances between Venus and
the center of the Sun
J.-E.
Arlot, P. Rocher (IMCCE) jeudi 13 janvier 2005
I.Introduction
In this
sheet we will give a simple formula allowing to calculate an approximation of
the solar parallax (and thus the Astronomical Unit or AU) starting from the
observation of the distance between Venus and the center
of the Sun. Contrary to the case of the contacts for which we need two
observations from distant sites, we will use only one observation with the
method known as “linear” which compares the observed value of this distance
with the calculated theoretical one. The difference between these two values
will enable us to correct the value of the theoretical solar parallax used in
calculations. It is in fact an iterative method but we will limit ourselves to
the last iteration. The goal – educational- of this calculation, is to show that
the value of the calculated AU depends on the quality of the measurement of
distance and also of the place of the observation. It will be interesting to
make several calculations starting from observations made at various moments
from the same place or distant places to compare the values obtained and to
average them.
Pre-calculated coefficients
To obtain this
formula, we pre-calculated parameters A, B, C and D which do not depend on the
position of the observers but which account for the motions of Venus and the
Earth around the Sun as well as the rotational movement of the Earth around its
axis. Attention, they depend on time and were tabulated consequently. The
parameter dD/dt represents the instantaneous
variation of the distance from the Venus center to
the center of the Sun. One can thus calculate the
theoretical value of the measured distance and reduce the observation (by
determining a new value of the parallax - or of the AU-) by taking account of
the fact that the observers, the centers of Venus,
the Earth and the Sun are not in the same plan and by using the relationship
between the distances of the Earth and Venus to the Sun given by the third law
of Kepler. One will find these tables at the end of
this sheet.
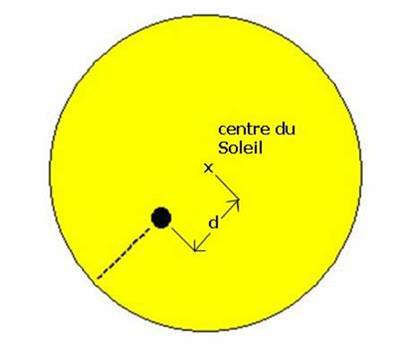
Measured
value d
between Venus and the centre of the Sun
II Observation of the
distance of Venus to the centre of the Sun
You must know the following quantities :
1. latitude and longitude
of the site of observation (l, j)
2. the distance from the
centre of Venus to the centre of the Sun (cf. figure above) in minutes of
degree
3. the date of the
observation in Universal Time (UTC) within one second of time
Formulae to be applied are as follows :
- transformation of the geographic latitude j of the site into geocentric latitude j‘ :
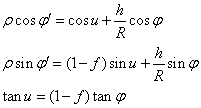
where h is
the elevation of the site, R the
terrestrial radius (taken as 6378,140 km) and
f the flatness of the Earth
(taken as 1/298.257)
and where cos
u and sin u are deduced from tan u
- calculation of the approximate value Dp of
the theoretical distance Dc
Venus-Sun using the pre-calculated coefficients A, B, C and D provided at the
end of the present sheet
![]() (F2)
(F2)
where p0 =
8,79414" and where r cos j’ and r sin j’ are calculated as above
Attention: if you wish to make a
more precise calculation, you need the accurate value of the theoretical
distance Dc . For that
purpose, you should use an ephemerides server such as
the one of http://www.imcce.fr,
calculating the positions of the center of the Sun
and the center of Venus at the date of the image and
deducing the distance Dc
from these positions.
- calculation of the new solar parallax, i.e.
the new value of the AU :
In order to reduce this observation
we will use the next formula:
![]() (F3)
(F3)
where D0
corresponds to our measure d given in
seconds of degree and A, B, C, dD/dt given
at the end of the present sheet
The solar parallax deduced from our
observation becomes : p0 + dp0 i.e. 8,79414 + dp0
In order to make the calculation, please fill
in the following form “distance”.
Calculating form « distance » :
Calculation of the solar parallax thanks to the observation of the
distance between Venus and the centre of the Sun
(in order to get a good result, you must average
several calculations using different observations)
geographic
longitude l =
geographic
latitude j =
observed
distance (Venus – Sun) : d =
in minutes of degree
date
of the observation in Universal Time (UTC) =
- transformation
of the geoghraphic latitude into geocentric latitude :
(1) geographic latitude
j
=
(2) Calculate the
cosine of j : cos (j ) =
(3) Calculate the
sine of j : sin (j) =
(4) Elevation of
the site of observation h = in
meters
(5) Calculate tan u
= (1 – 1/298,257) x tan (line (1)) =
(6) Calculate the
angle u (which remains between -90° and +90°) = arctan
(line(5)) =
(7) Calculate the
cosine of u = cos (line(6))
=
(8) Calculate the
sine of u = sin (line(6)) =
(9) Calculate (r cos
j’)
= cos u + (h/6378140) cos j
= line (7) + [(line (4)/6378140) x line (2)] =
(10) Calculate (r sin j’) = (1 –
1/298,257) x sin u + ( h / 6378140 ) sin j
= (1 – 1/298,257) x line (8) +
[(line(4) / 6378140) x line (3)] =
- calculation of
the theoretical distance « Venus-Sun » (if you prefer to use
an ephemerides server, go to line 20):
(11) Calculate the
cosine of l : cos l =
(12) Calculate the
sine of l : sin l =
(13) Calculate (r cos
j’
cos l) = line (9) x line (11) =
(14) Calculate (r cos
j’
sin l) = line (9) x line (12) =
(15) Détermine A from the table at the end of the sheet : A
=
(16) Détermine B from the table at the end of the
sheet : B =
(17) Détermine C from the table at the end of the
sheet : C =
(18) Calculate the
coefficient of p0 in formula
(F2) :
= line (15) x line (13) + line (16) x line (14) +line
(17) x line (10) =
(19) Détermine D from the table at the end of the
sheet : D =
(20) Calculate the
second member of formula (F2) i.e. the value of Dtheoretical :
= line (19) + 8.79414 x line (18) =
- calculation of
the new solar parallax :
(21) Your measure
of dobserved in seconds of degree =
(22) Difference
« observed – calculated » = line (21) – line (20) =
(23) Correction of
the parallax deduced from the observation = line (22) / line (18) =
(24) New value of
the solar parallax p0 = 8.79414 + line
(25) =
- calculation of
the astronomical unit :
(25) Calculate the
astronomical unit :
AU = line (24) x (206265.806247 / 6 378.1363) =
You may remake the
same calculation using other observed distances Venus-Sun either made from the
same site, or made from another site of observation, and make an average of all
the results.
Remind you that the proposed method
of calculation is an approximation and, in order to get a more accurate result,
you must use more complete formulae (as given in sheets n°4 and 5). Even if your observation was perfect, you will
get only an approximation of the AU.
Pre-calculated
coefficients to be used in the above formulae :
The two following tables provide the
values of the parameters A, B, C, dD/dt,
D depending on time every 5 minutes de temps during the transit. The three
first parameters are without dimension, dD/dt
is in seconds of degree / minute of time, D is in minutes of degree.
|
T UTC |
A |
B |
C |
dD/dt |
D ' |
|
5h05m |
2.2768 |
-0.1279 |
0.9656 |
-3.1409 |
16.6791 |
|
5h10m |
2.2682 |
-0.0645 |
0.9919 |
-3.1085 |
16.4202 |
|
5h15m |
2.2571 |
-0.0011 |
1.0189 |
-3.0746 |
16.1641 |
|
5h20m |
2.2436 |
0.0622 |
1.0465 |
-3.0389 |
15.9108 |
|
5h25m |
2.2275 |
0.1254 |
1.0749 |
-3.0016 |
15.6606 |
|
5h30m |
2.2088 |
0.1882 |
1.1039 |
-2.9624 |
15.4135 |
|
5h35m |
2.1874 |
0.2507 |
1.1336 |
-2.9214 |
15.1697 |
|
5h40m |
2.1634 |
0.3128 |
1.1640 |
-2.8783 |
14.9295 |
|
5h45m |
2.1365 |
0.3742 |
1.1951 |
-2.8331 |
14.6928 |
|
5h50m |
2.1067 |
0.4350 |
1.2269 |
-2.7857 |
14.4601 |
|
5h55m |
2.0741 |
0.4950 |
1.2594 |
-2.7359 |
14.2313 |
|
6h00m |
2.0385 |
0.5540 |
1.2925 |
-2.6837 |
14.0068 |
|
6h05m |
1.9998 |
0.6119 |
1.3263 |
-2.6290 |
13.7867 |
|
6h10m |
1.9581 |
0.6686 |
1.3607 |
-2.5716 |
13.5712 |
|
6h15m |
1.9133 |
0.7239 |
1.3957 |
-2.5115 |
13.3607 |
|
6h20m |
1.8653 |
0.7776 |
1.4313 |
-2.4484 |
13.1552 |
|
6h25m |
1.8142 |
0.8297 |
1.4674 |
-2.3824 |
12.9550 |
|
6h30m |
1.7598 |
0.8797 |
1.5040 |
-2.3133 |
12.7605 |
|
6h35m |
1.7022 |
0.9277 |
1.5410 |
-2.2411 |
12.5718 |
|
6h40m |
1.6414 |
0.9734 |
1.5783 |
-2.1655 |
12.3892 |
|
6h45m |
1.5774 |
1.0166 |
1.6159 |
-2.0866 |
12.2131 |
|
6h50m |
1.5103 |
1.0570 |
1.6537 |
-2.0043 |
12.0436 |
|
6h55m |
1.4400 |
1.0945 |
1.6916 |
-1.9185 |
11.8811 |
|
7h00m |
1.3667 |
1.1288 |
1.7294 |
-1.8291 |
11.7258 |
|
7h05m |
1.2904 |
1.1598 |
1.7671 |
-1.7363 |
11.5781 |
|
7h10m |
1.2113 |
1.1871 |
1.8045 |
-1.6399 |
11.4382 |
|
7h15m |
1.1295 |
1.2107 |
1.8415 |
-1.5401 |
11.3064 |
|
7h20m |
1.0452 |
1.2302 |
1.8780 |
-1.4368 |
11.1831 |
|
7h25m |
0.9586 |
1.2455 |
1.9138 |
-1.3301 |
11.0684 |
|
7h30m |
0.8699 |
1.2564 |
1.9488 |
-1.2203 |
10.9628 |
|
7h35m |
0.7793 |
1.2628 |
1.9827 |
-1.1073 |
10.8663 |
|
7h40m |
0.6872 |
1.2644 |
2.0154 |
-0.9914 |
10.7794 |
|
7h45m |
0.5938 |
1.2612 |
2.0469 |
-0.8729 |
10.7021 |
|
7h50m |
0.4995 |
1.2531 |
2.0768 |
-0.7520 |
10.6348 |
|
7h55m |
0.4046 |
1.2400 |
2.1051 |
-0.6289 |
10.5776 |
|
8h00m |
0.3095 |
1.2220 |
2.1316 |
-0.5039 |
10.5306 |
|
8h05m |
0.2147 |
1.1989 |
2.1563 |
-0.3775 |
10.4941 |
|
8h10m |
0.1204 |
1.1709 |
2.1789 |
-0.2499 |
10.4681 |
|
8h15m |
0.0271 |
1.1380 |
2.1993 |
-0.1216 |
10.4527 |
|
8h20m |
-0.0647 |
1.1004 |
2.2176 |
0.0071 |
10.4480 |
|
8h25m |
-0.1548 |
1.0583 |
2.2336 |
0.1357 |
10.4539 |
|
8h30m |
-0.2428 |
1.0118 |
2.2473 |
0.2640 |
10.4704 |
|
8h35m |
-0.3282 |
0.9611 |
2.2586 |
0.3914 |
10.4976 |
|
8h40m |
-0.4108 |
0.9065 |
2.2677 |
0.5177 |
10.5353 |
|
8h45m |
-0.4901 |
0.8484 |
2.2744 |
0.6424 |
10.5833 |
T UTC |
A |
B |
C |
dD/dt |
D ' |
|
8h50m |
-0.5661 |
0.7869 |
2.2789 |
0.7653 |
10.6417 |
|
8h55m |
-0.6383 |
0.7224 |
2.2811 |
0.8860 |
10.7101 |
|
9h00m |
-0.7067 |
0.6552 |
2.2813 |
1.0043 |
10.7884 |
|
9h05m |
-0.7709 |
0.5857 |
2.2794 |
1.1198 |
10.8764 |
|
9h10m |
-0.8310 |
0.5141 |
2.2755 |
1.2324 |
10.9739 |
|
9h15m |
-0.8867 |
0.4409 |
2.2699 |
1.3419 |
11.0806 |
|
9h20m |
-0.9380 |
0.3663 |
2.2625 |
1.4482 |
11.1962 |
|
9h25m |
-0.9849 |
0.2905 |
2.2535 |
1.5511 |
11.3204 |
|
9h30m |
-1.0273 |
0.2140 |
2.2432 |
1.6506 |
11.4531 |
|
9h35m |
-1.0653 |
0.1370 |
2.2314 |
1.7466 |
11.5938 |
|
9h40m |
-1.0989 |
0.0598 |
2.2185 |
1.8390 |
11.7424 |
|
9h45m |
-1.1281 |
-0.0175 |
2.2045 |
1.9279 |
11.8985 |
|
9h50m |
-1.1531 |
-0.0945 |
2.1896 |
2.0133 |
12.0618 |
|
9h55m |
-1.1740 |
-0.1711 |
2.1738 |
2.0953 |
12.2320 |
|
10h00m |
-1.1908 |
-0.2471 |
2.1573 |
2.1738 |
12.4089 |
|
10h05m |
-1.2036 |
-0.3222 |
2.1402 |
2.2490 |
12.5921 |
|
10h10m |
-1.2127 |
-0.3964 |
2.1225 |
2.3209 |
12.7814 |
|
10h15m |
-1.2181 |
-0.4696 |
2.1044 |
2.3896 |
12.9766 |
|
10h20m |
-1.2200 |
-0.5414 |
2.0860 |
2.4553 |
13.1773 |
|
10h25m |
-1.2184 |
-0.6120 |
2.0673 |
2.5180 |
13.3833 |
|
10h30m |
-1.2137 |
-0.6811 |
2.0484 |
2.5778 |
13.5945 |
|
10h35m |
-1.2058 |
-0.7488 |
2.0293 |
2.6349 |
13.8104 |
|
10h40m |
-1.1950 |
-0.8148 |
2.0102 |
2.6893 |
14.0310 |
|
10h45m |
-1.1813 |
-0.8792 |
1.9911 |
2.7412 |
14.2560 |
|
10h50m |
-1.1649 |
-0.9419 |
1.9719 |
2.7907 |
14.4852 |
|
10h55m |
-1.1460 |
-1.0028 |
1.9529 |
2.8379 |
14.7183 |
|
11h00m |
-1.1247 |
-1.0620 |
1.9339 |
2.8828 |
14.9553 |
|
11h05m |
-1.1010 |
-1.1194 |
1.9151 |
2.9257 |
15.1960 |
|
11h10m |
-1.0752 |
-1.1749 |
1.8964 |
2.9665 |
15.4401 |
|
11h15m |
-1.0473 |
-1.2286 |
1.8779 |
3.0055 |
15.6875 |
|
11h20m |
-1.0175 |
-1.2804 |
1.8596 |
3.0426 |
15.9380 |
|
11h25m |
-0.9858 |
-1.3303 |
1.8415 |
3.0780 |
16.1916 |
|
11h30m |
-0.9524 |
-1.3783 |
1.8237 |
3.1118 |
16.4480 |
|
11h35m |
-0.9174 |
-1.4244 |
1.8061 |
3.1440 |
16.7072 |