Fiche pédagogique n° 02a:
La géométrie et la prédiction des passages de Vénus
devant le Soleil.
P. Rocher (IMCCE)
I. Introduction.
On peut considérer le passage d’une planète devant le Soleil suivant deux approches. Nous allons les décrire elles ont un intérêt pédagogique important. La première approche nous montre les passages de Vénus, vus en quelque sorte de l’extérieur, elle fait appel aux mêmes notions que les éclipses de Soleil : l’ombre et la pénombre générées par un corps éclairé par le Soleil. La seconde est plus terrestre, on se place dans un premier temps au centre de la Terre, puis on calcule grâce à la parallaxe les circonstances en un lieu quelconque du globe terrestre.
II. L’approche héliocentrique : la Terre passe dans le prolongement de l’ombre et la pénombre de Vénus.
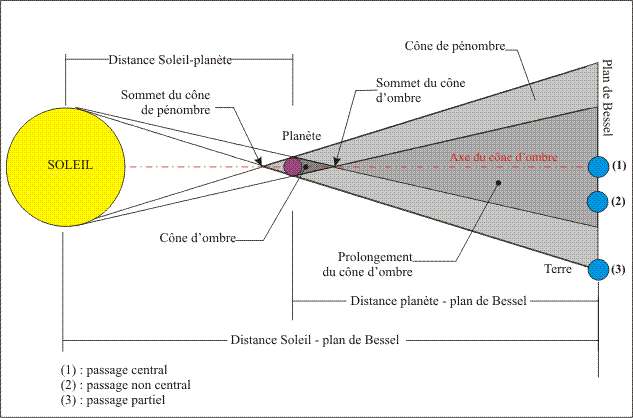
Figure 1. – Approche « éclipse de Soleil » d’un passage de Vénus.
La planète Vénus, éclairée par le Soleil, donne naissance, dans la direction opposée au Soleil à deux cônes, un cône d'ombre et un cône de pénombre. La droite joignant le centre du Soleil et le centre de Vénus constitue l'axe de ces cônes. Le sommet du cône de pénombre est situé sur cet axe entre le Soleil et Vénus, et le sommet du cône d'ombre est également situé sur cet axe mais de l'autre côté par rapport Vénus. Un observateur placé dans le cône d'ombre, avant son sommet verrait une éclipse totale du Soleil par Vénus, un observateur situé dans le prolongement du cône d'ombre, donc après le sommet du cône d'ombre, voit une éclipse annulaire du Soleil par Vénus, donc un passage de Vénus devant le Soleil. Un observateur se trouvant dans le cône de pénombre assiste à une éclipse partielle du Soleil par Vénus, donc à un passage partiel de Vénus devant le Soleil. En raison de la distance entre la Terre et Vénus, la Terre passe uniquement dans le prolongement du cône d'ombre et dans le cône de pénombre. Cela se traduit pour un observateur terrestre par l'observation d'un passage de Vénus devant le disque solaire (éclipse annulaire) compris entre deux phases partielles (entrée et sortie de Vénus du disque solaire). On peut également avoir uniquement un passage de la Terre dans la pénombre, dans ce cas on n'observe qu'une phase partielle d'éclipse, donc le passage d'une partie du disque de Vénus devant le disque solaire.
Si l’orbite de Vénus était dans le plan de l'écliptique (plan de l'orbite de la Terre), il y aurait un passage de la Terre dans l’ombre de Vénus (donc un passage de Vénus devant le Soleil) chaque fois que Vénus est en conjonction inférieure en longitude avec la Terre, donc avec une périodicité égale à la révolution synodique de Vénus. La révolution synodique est l'intervalle de temps qui s'écoule entre deux passages successifs d'une planète dans une position déterminée par rapport au Soleil et à la Terre (conjonction ou opposition). L'inclinaison de l'orbite de Vénus (~3,39°) limite la possibilité des passages aux voisinages de la ligne des nœuds des orbites. La ligne des nœuds est la droite formée par l'intersection du plan orbital de la planète et le plan de l'orbite terrestre.
Le plan de Bessel est le plan passant par le centre de la Terre et normal à l'axe des cônes (voir figure 1). Les intersections des cônes d'ombre et de pénombre avec le plan de Bessel déterminent des cercles d'ombre et de pénombre. La comparaison des rayons de ces cercles avec la distance entre l'axe des cônes et le centre de la Terre permet de savoir si la Terre pénètre dans les cônes d'ombre et de pénombre, donc de savoir si le passage est observable ou non.
Si les planètes avaient des trajectoires circulaires autour du Soleil, la géométrie du problème serait figée et les tailles des cônes d'ombre et de pénombre, ainsi que la position de leurs sommets, seraient constantes dans le temps. En réalité les planètes parcourent des trajectoires elliptiques perturbées et les distances Soleil-planètes ne sont pas constantes. Les plus grandes valeurs des angles au sommet des cônes d'ombre et de pénombre de Vénus correspondent aux minima des distances Soleil-Vénus (Vénus au périhélie) et les plus petites valeurs correspondent aux maxima des distances Soleil-Vénus (Vénus à l'aphélie). En réalité comme les passages ne sont observables qu'au voisinage des nœuds de l’orbite, il convient de calculer les dimensions des cônes d'ombre et de pénombre au voisinage des nœuds de l’orbite de Vénus. En raison des perturbations, la ligne des nœuds de Vénus, ainsi que sa ligne des apsides (ligne joignant le périhélie et l'aphélie), ne sont pas fixes, mais sont animées de faibles mouvements de précession. La période de révolution correspondant à deux passages de Vénus par le même nœud de l'orbite s'appelle révolution draconitique et la période de révolution correspondant à deux passages de Vénus à son périhélie s'appelle révolution anomalistique.
Les passages de Vénus ont donc lieu aux voisinages des passages de la Terre par les nœuds de l'orbite de Vénus. Entre 1200 et 2800, la Terre passe par le nœud descendant de l'orbite de Vénus dans la première moitié du mois de juin et par le nœud ascendant dans la première moitié du mois de décembre.
Par le passé, lorsque les calculs étaient faits à la main, on se contentait de calculer les phases géocentriques des passages, c'est-à-dire les instants des entrées et des sorties du centre de la Terre des cônes de pénombre et d'ombre (figure 1). Et l'on traçait sur un planisphère les limites de visibilité du phénomène, c'est-à-dire les courbes des lieux ayant la planète à l'horizon au moment de l'entrée et de la sortie du cône de pénombre. On calculait également la distance angulaire géocentrique minimale entre le centre du Soleil et le centre de la planète. Ce minimum, parfois nommé maximum du passage, caractérise en quelque sorte la grandeur du passage. Pour l'édition des instants des différentes phases géocentriques, et pour des raisons de symétrie, on se limitait souvent à donner l'instant du maximum du passage et les demi-durées des phases d'ombre et de pénombre. Lorsqu'on se limite aux calculs des phases géocentriques, on ne trouve pas les passages partiels ne couvrant qu'un demi-hémisphère terrestre et ne passant pas par le centre de la Terre.
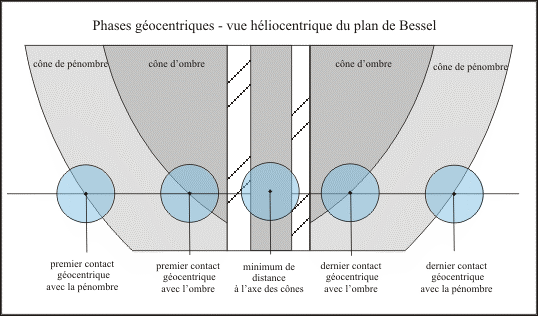
Figure 2. – Phases géocentriques des passages de Vénus.
De nos jours, grâce à l'informatisation des calculs, il est possible de faire des calculs plus rigoureux et de déterminer les instants et positions des différents contacts entre les cônes d'ombre et de pénombre et la surface de l'ellipsoïde terrestre. Ces instants sont les phases générales du passage (figure 3). Chaque phase, comme pour les éclipses de Soleil, correspond à un instant particulier et à un lieu bien défini sur la Terre. Ces phases générales tiennent compte des parallaxes solaire et planétaire.
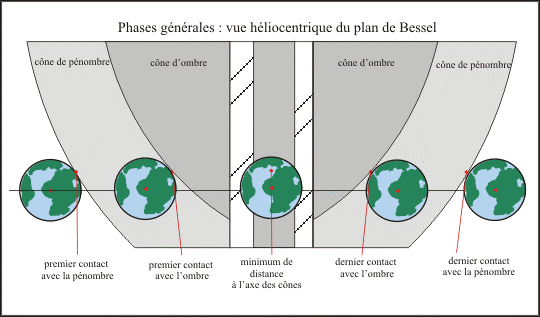
Figure 3. – Phases générales des passages de Vénus.
Les phases générales sont légèrement plus longues que les phases géocentriques, les différences de durée correspondent au temps mis par l'ombre ou la pénombre pour passer du point de contact au centre de la Terre. Ces écarts ne sont pas constants, mais varient avec les vitesses relatives de la planète et de la Terre et avec la position des points de contact sur les bords de l'ombre et de la pénombre. Les différences de taille entre les rayons des cônes d'ombre et de pénombre montrent qu'il peut y avoir des passages où la Terre passe uniquement dans le cône de pénombre, dans ce cas on observe de la Terre un passage partiel du disque de la planète sur le disque solaire. Lorsque la Terre rencontre l'axe des cônes, il existe des lieux sur Terre où la planète lors de son passage devant le Soleil passe exactement par le centre du disque solaire, ces passages seront notés passages centraux. Tous les autres passages, et ce sont les plus fréquents, sont des passages non-centraux.
Sur les figures 2 et 3 on remarquera que les passages des cônes d’ombre et de pénombre se font d’est en ouest sur la Terre, car la vitesse de Vénus étant plus rapide que celle de la Terre il en est de même pour son ombre, qui rattrape la Terre et la dépasse en venant de l’est.
En conclusion, il y a trois types de passages, les passages centraux, les passages non-centraux et les passages partiels (figure 4).
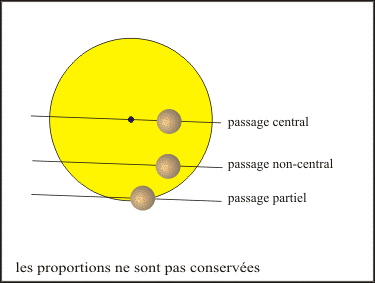
Figure 4. – Les trois types de passages possibles.
Cet aspect des passages de Vénus devant le Soleil présente certains avantages. Le premier est la parfaite similitude entre une éclipse de Soleil et un passage de Vénus, le rôle de la Lune étant joué par Vénus. On peut ainsi réutiliser tous les formulaires propres aux éclipses de Soleil en remplaçant la Lune par Vénus. L’autre intérêt est la détermination directe des circonstances générales du passage qui ne nécessite pas un calcul préalable des circonstances géocentriques. Enfin le calcul des circonstances locales d’observations du passage en un lieu donné peut être fait en utilisant les méthodes propres aux éclipses solaires c’est-à-dire en utilisant les éléments dits de Bessel. Par contre cet aspect présente un inconvénient, comme aucun lieu n’est privilégié pour le calcul des circonstances locales, les différences de parallaxe n’apparaissent pas explicitement dans les calculs. Ce qui rend l’opération inverse, passer de l’observation à la valeur de la parallaxe, plus complexe.
III. L’approche géocentrique.
Cette approche des passages est souvent privilégiée car elle est plus simple et ne nécessite pas d’avoir une vue extérieure du phénomène.
L’observateur, dans un premier temps se place au centre de la Terre. On ramène les mouvements observés à un repère terrestre géocentrique. Vue depuis le centre de la Terre, l’orbite apparente du Soleil est une ellipse située dans le plan de l’écliptique (plan de l’orbite terrestre), l’orbite apparente de Vénus est par contre beaucoup plus complexe. Vue depuis la Terre on distingue plusieurs configurations :
§ La longitude de Vénus est la même que la longitude du Soleil : on a une conjonction inférieure si Vénus est entre le Soleil et la Terre et on a une conjonction supérieure si le Soleil est entre Vénus et la Terre.
§ La distance angulaire entre le Soleil et Vénus est maximale : c’est une plus grande élongation. Si la planète est à l’ouest du Soleil (plus grande élongation ouest) la planète est visible le matin avant le lever du Soleil et elle n’est pas visible le soir car elle se couche avant le Soleil. Si la planète est à l’est du Soleil (plus grande élongation est) la planète est visible le soir après le coucher du Soleil et est invisible le matin car elle se lève après le Soleil.
§ Vénus passe dans le plan de l’orbite apparente du Soleil : c’est un passage aux nœuds de son orbite ; si elle passe d’en dessous de l’écliptique à au-dessus de l’écliptique on a un passage au nœud ascendant et si elle passe d’au-dessus de l’écliptique à en dessous de l’écliptique on a un passage au nœud descendant.
§ La distance entre Vénus et la Terre est minimale, par abus de langage, on appelle ce moment le passage au périgée. Le diamètre apparent de Vénus est maximal.
§ La distance entre Vénus et la Terre est maximale, par abus de langage, on appelle ce moment le passage à l’apogée. Le diamètre apparent de Vénus est minimal.
§ Vénus est stationnaire par rapport aux étoiles puis change de direction par rapport aux étoiles (mouvement direct ou rétrograde).
§ La distance de Vénus au Soleil est minimale (passage au périhélie) ou maximale (passage à l’aphélie).
Pour avoir un passage de Vénus devant le Soleil, il faut réunir deux de ces phénomènes : un alignement en longitude de Vénus et du Soleil avec Vénus entre le Soleil et la Terre (conjonction inférieure) et la planète Vénus pas trop haute au-dessus ou en dessous de l’écliptique donc proche d’un de ces nœuds.
Remarque : si l’on a une conjonction supérieure proche d’un passage aux nœuds on assiste à un passage de Vénus derrière le disque solaire. Ce phénomène aurait un intérêt s’il était facilement observable, ce qui n’est pas le cas.
IV. La prédiction des passages de Vénus.
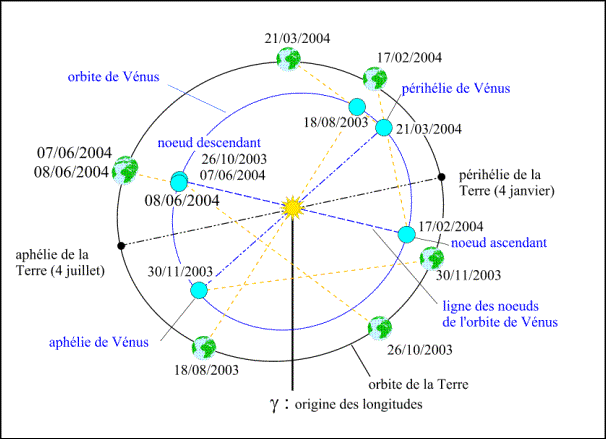
Figure 5. – Positions de Vénus et de la Terre entre le
18/08/2003 et le 08/06/2004.
La figure 5 et la liste suivante nous donnent les principaux phénomènes astronomiques liés à Vénus depuis sa dernière conjonction supérieure le 18 août 2003 jusqu’à son passage devant le Soleil le 8 juin 2004.
§ le 18/08/2003 à 18h 04m 33s UTC : Vénus en conjonction supérieure, diamètre apparent =9.6", latitude géocentrique. = + 1° 18,8'.
§ le 26/10/2003 à 22h 08m 54s UTC : Vénus passe par le nœud descendant de son orbite, longitude moyenne géocentrique = +231° 19,9'.
§ le 30/11/2003 à 12h 18m 44s UTC : Vénus à l'aphélie (distance maximale au Soleil) d = 0,72820 ua.
§ le 17/02/2004 à 01h 27m 45s UTC : Vénus passe par le nœud ascendant de son orbite, longitude moyenne géocentrique = + 9° 50,4'.
§ le 21/03/2004 à 21h 57m 13s UTC : Vénus au périhélie (distance minimale au Soleil) d = 0,71845 ua.
§ le 18/05/2004 à 00h 29m 30s UTC : Vénus est stationnaire dans la constellation du Taureau, puis rétrograde.
§ le 07/06/2004 à 14h 48m 05s UTC : Vénus passe par le nœud descendant de son orbite, longitude moyenne géocentrique = +78° 21,6'.
§ le 08/06/2004 à 06h 52m 00s UTC : Vénus au périgée (distance minimale à la Terre) d = 0.28888 ua, diamètre apparent = 57.8".
§ le 08/06/2004 à 08h 43m 05s UT : Vénus en conjonction inférieure, diamètre apparent = 57.8", latitude géocentrique. = - 0° 10,6'.
Comme on le constate trois phénomènes sont très proches les uns des
autres, le passage de Vénus par son nœud descendant, puis la plus petite
distance entre la Terre et Vénus et enfin la conjonction inférieure de Vénus.
On remarque également que la valeur absolue de la latitude de Vénus (10,6') au
moment de la conjonction inférieure est plus petite que le demi-diamètre
apparent moyen du Soleil (15,5') donc au moment de la conjonction en longitude
le disque de Vénus est devant le disque solaire.
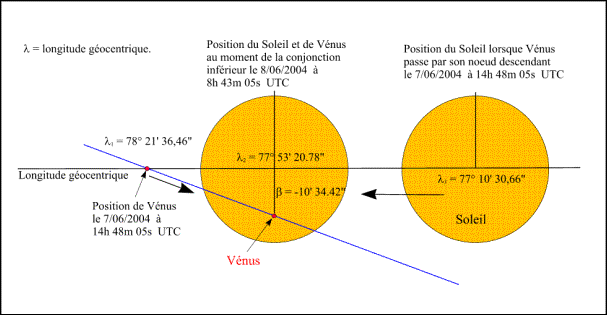
Figure 6. – Circonstances géocentriques du passage de Vénus du 8 juin 2004.
On constate également que la conjonction a lieu après le minimum de distance géocentrique entre le centre de Vénus et le centre du Soleil. La figure 6 donne les positions respectives de Vénus et du Soleil au moment du passage de Vénus par son nœud descendant et au moment de la conjonction en longitude.
Cet aspect du passage présente un avantage, en travaillant dans le plan tangent à la sphère céleste et normal à la direction centre de la Terre – centre du Soleil on se ramène à un problème plan. Par contre il privilégie un point particulier : le centre de la Terre. On peut calculer pour le centre de la Terre les instants des contacts extérieurs et intérieurs de Vénus avec le disque solaire. Les contacts extérieurs correspondent aux instants où la distance entre les centres géocentriques des astres est égale à la somme de leurs demi-diamètres apparents et les contacts intérieures correspondent aux instants où la distance entre les centres des astres est égale à la différence de leurs demi-diamètres apparents. Ils sont identiques aux instants où le centre de la Terre entre et sort des cônes de pénombre et d’ombre de Vénus.
Comment calculer les circonstances locales du passage pour un lieu quelconque à la surface de la terre ?
Il y a deux manières de procéder.
Première méthode : On peut faire un calcul direct identique au calcul géocentrique, mais en se plaçant au lieu considéré. Ce calcul est plus complexe que le précédent car on doit tenir compte du mouvement de rotation de l’observateur à la surface de la Terre.
Seconde méthode : On utile la différence de parallaxe entre le lieu et le centre de la Terre à l’instant des contacts géocentriques pour en déduire les instants des contacts locaux.
La première méthode plus complexe permet de faire un calcul rigoureux. Elle nécessite plus de calcul mais ce n’est pas un problème de nos jours. La seconde méthode plus simple donne des résultats plus ou moins précis en fonction des simplifications et des linéarisations que l’on utilise. Elle est amplement suffisante pour prédire les contacts au dixième de minute près et pour tracer les cartes de visibilité.
V. Les périodes de récurrence dans les passages de Vénus.
Nous avons construit à l’IMCCE des canons de passages contenant tous les passages des planètes Mercure et Vénus devant le Soleil sur une période de 6000 ans allant de l’an –3000 à l’an 3000.
À l'aide de ces canons, on peut rechercher des périodes de récurrence dans
les dates des passages. Ces périodes sont identiques au "saros" pour
les éclipses de Lune et de Soleil. Ces périodes sont toujours des multiples
communs de la révolution synodique et de la révolution draconitique de Vénus.
La révolution synodique ramène Vénus et la Terre en conjonction et la
révolution draconitique ramène Vénus au nœud de son orbite. Néanmoins cette
relation simple entre révolution synodique et draconitique n'est pas suffisante
pour que les passages se répètent avec la fréquence trouvée. En effet il faut
en plus que la position de la Terre au moment du passage de Vénus par son nœud,
c'est-à-dire pour le multiple de la révolution draconitique considéré, se
trouve encore à l'intérieur d’un segment angulaire qui définit un critère
d'observation, c’est-à-dire un critère permettant de savoir si le passage est
observable où non. Cette dernière contrainte fait intervenir la période de
révolution moyenne ramenant la Terre aux nœuds de l'orbite de Vénus. Par
analogie avec l'étude des éclipses de Lune et de Soleil où cette période
s'appelle "saison des éclipses", nous l'appelons "saison des
passages de Vénus". Cette période moyenne se calcule en combinant le
mouvement moyen de la Terre et le mouvement de la ligne des nœuds de l’orbite
de Vénus.
On peut trouver les multiples communs aux révolutions synodique et draconitique, en décomposant le rapport de ces deux révolutions sous forme de fractions continues. Le but de cette décomposition créée par Laplace en 1768 est d'obtenir les approximations d'un nombre réel positif sous la forme de quotients de deux nombres entiers.
Pour Vénus la saison des passages est égale à 365,25133208 jours et le rapport de la révolution synodique (583,9213609 jours) sur la révolution draconitique (224,6988946 jours) est égal à 2,598683727 On trouve une période de récurrence de 243 ans. Comme avec les éclipses de Lune et de Soleil on peut construire des séries longues de passages homogènes dont chaque passage est séparé par cette période de 243 ans. Chacune de ces séries a toujours lieu au même nœud ; les séries au nœud descendant comportent environ 24 passages et les séries de passages au nœud ascendant comportent environ 20 passages.
Par la méthode de décomposition en fractions continues, on ne trouve pas les périodes non entières qui apparaissent dans la succession des passages de Vénus, c'est à dire les périodes de 105.5 ans et 121.5 ans. Ces périodes qui ne sont pas de vraies périodes de récurrence introduisent une alternance de nœuds dans les passages. Ainsi la période de 243 ans se décompose parfois sous la forme de quatre passages se succédant avec le cycle suivant : 8ans, 121.5 ans, 8 ans, 105.5 ans. Mais ce cycle contrairement à ce que l’on affirme souvent n’est pas immuable, il présente des ruptures sur des périodes très longues.
Sur l figure 7, on a porté en ordonnée les distances du centre de Vénus au centre du Soleil en fonction des dates des passages qui figurent en abscisse. Les séries de passages aux nœuds ascendants sont en bleu et celles des passages au nœud descendant sont en rouge, la période de représentation est de 6000 ans (-3000 à +3000). On a tracé en vert et en violet les sauts de 8 ans entre passages identiques, on constate bien deux ruptures de saut, une pour le nœud descendant entre -920 et 546 et une au nœud descendant entre -548 et 1631, ce qui fait une rupture du cycle (8ans, 121.5 ans, 8 ans, 105.5 ans) entre -920 et 1631 soit 25 siècles et demi ! On a tracé en jaune les passages successifs respectant le cycle (8ans, 121.5 ans, 8 ans, 105.5 ans). On voit que ce cycle a repris depuis le début du XVIe siècle.
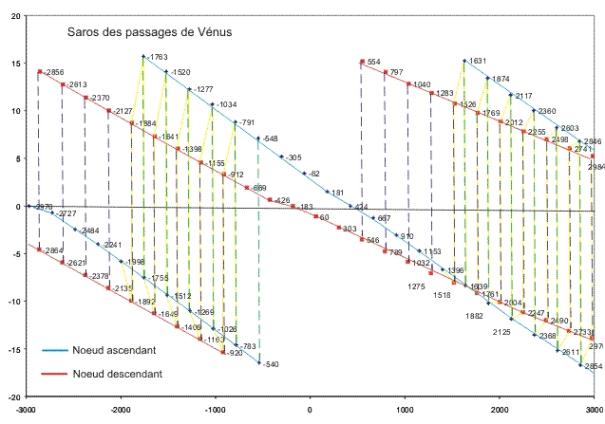
Figure 7. – Saros des passages de Vénus.