Fiche pédagogique n° 03 :
Les prédictions du passage de Vénus du 8 juin 2004
P. Rocher (IMCCE)
I. Introduction
Nous donnons dans ce document les prédictions du passage de Vénus devant le Soleil du 8 juin 2004. Ces prédictions sont faites à l’aide des théories planétaires VSOP87 élaborées à l’IMCCE Les précisions des positions des planètes intérieures dans ces théories est de l’ordre de 0,005 seconde de degré. L’obtention des coordonnées apparentes des astres nécessitent l’usage de théories de la précession et de la nutation et du temps sidéral. Nous avons utilisé la théorie de la précession de Lieske (1976), la théorie de la nutation de Wahr (1981) et le temps sidéral d’Aoki (1992).
Ces prédictions dépendent également d’un certain nombre de paramètres physiques qui doivent être cohérents entre eux et avec les théories planétaires utilisées.
Comme les théories VSOP87 utilisent la valeur de l’unité astronomique de l’UAI 1976 (a = 149 597 870 km ) nous avons utilisé également les constantes UAI 1976 pour le demi-diamètre équatorial terrestre (R = 6 378,140 km) et pour la valeur de la parallaxe équatoriale horizontale moyenne du Soleil (p0 = 8.794148"= R/a). Nous avons également pris les constantes UAI 1976 pour le demi-diamètre solaire à une unité astronomique (d = 15° 59,63') et pour le demi-diamètre de Vénus (d’=6051.8 km). L’aplatissement terrestre est pris égal à 1/298,257 (IERS 1992). Pour ces calculs, comme pour l’élaboration de nos canons de passages de Mercure et Vénus, nous avons utilisé un formulaire identique à celui des éclipses solaires utilisant les éléments de Bessel.
Il existe trois types d’information : les circonstances générales du passage, les circonstances géocentriques du passage et enfin les circonstances locales du passage. Dans tous les cas l’échelle de temps utilisée dans les prédictions est le temps universel coordonné (UTC ou UT), l’écart entre le temps terrestre (TT) et le temps universel coordonné (TT–UTC) a été pris égal à 65,184s.
Dans nos tableaux les
longitudes géographiques sont toujours comptées positivement vers l’ouest et
négativement vers l’est.
II. Les circonstances générales.
On donne les caractéristiques de la conjonction en longitude entre Vénus et le Soleil, c’est l’instant où les longitudes apparentes géocentriques de Vénus et du Soleil sont égales. Les circonstances générales du passage décrivent les contacts de l’ellipsoïde terrestre avec les bords des cônes de pénombre et d’ombre. Chaque contact correspond donc à un lieu particulier et à un instant particulier. Ce lieu de la surface terrestre est le point de tangence entre l’ellipsoïde et le cône d’ombre ou de pénombre au moment du contact. Le maximum du contact correspond à l’instant et au lieu sur Terre, où la distance entre ce lieu et l’axe des cônes est minimale ; ce lieu a Vénus à l’horizon à l’instant considéré. Nous donnons également pour chaque contact le lieu sur Terre qui a Vénus (ou le Soleil) à son zénith, cette direction permet de tracer le cercle de visibilité de Vénus à l’instant considéré.
Conjonction le 8 juin 2004 à 8h 43m 4.97s UTC. |
|
|
Longitude
géocentrique de Vénus |
77°
53' 20,783" |
|
Latitude
géocentrique de Vénus |
-0°
10' 34,42" |
|
Longitude
géocentrique du Soleil |
77°
53' 20,783" |
|
Latitude
géocentrique du Soleil |
-0°
0' 0,60" |
|
Parallaxe
équatoriale du Soleil |
8,66" |
|
Parallaxe
équatoriale de Vénus |
30,44" |
|
Demi-diamètre vrai
du Soleil |
15'
45,4" |
|
Demi-diamètre vrai
de Vénus |
28,88" |
Le diamètre apparent de Vénus est le trois centième du diamètre apparent du Soleil.
Phases générales
|
Phases |
Instant en
UTC |
Position des contacts |
Lieu
ayant la planète au zénith |
||
|
Longitude |
Latitude |
Longitude |
Latitude |
||
|
Premier contact de la pénombre |
5h 6m 30,5s |
+177° 25,7' |
-23° 12,9' |
-103°
24,1' |
+22°
45,4' |
|
Premier contact de l'ombre |
5h 25m 27,4s |
-176° 27,6' |
-25° 52,1' |
-
98° 38,6' |
+22°
45,2' |
|
Maximum du passage |
8h 19m 44,3s |
- 86° 39,9' |
-63° 29,9' |
-
54° 52,4' |
+22°
43,1' |
|
Dernier contact de l'ombre |
11h 13m
58,9s |
+ 48° 52,7' |
-49° 30,5' |
-
11° 6,8' |
+22°
41,0' |
|
Dernier contact de la pénombre |
11h 32m 56,0s |
+ 56° 11,2' |
-47° 8,5' |
-
6° 21,3' |
+22°
40,7' |
Durées des phases générales
Durée du passage général : 6h 26m 25,45s.
Durée du passage dans l'ombre : 5h 48m 31,49s.
Paramètres physiques des cônes d'ombre et de pénombre et élongation minimale
Rayon du cône d'ombre : 42,08 rayons terrestres.
Distance géocentrique du bord de l'ombre : 13,30 rayons terrestres.
Distance géocentrique du bord de la pénombre : 15,95 rayons terrestres.
Rayon du cône de pénombre : 44,73 rayons terrestres.
Distance minimale topocentrique entre les centres du Soleil et de Vénus : 10' 5,156".
III. Circonstances géocentriques.
Les circonstances géocentriques sont liées à un point bien particulier : le centre de l’ellipsoïde terrestre. On donne les instants des différents contacts, ces instants correspondent aux instants où, vu depuis le centre de la Terre, le disque apparent de Vénus est tangent extérieur ou intérieur au disque solaire. Ce sont également les instants où le centre de la Terre entre et sort des cônes d’ombre et de pénombre. Le maximum du passage est l’instant où, toujours vue depuis le centre de la Terre, la distance entre les centres de Vénus et du Soleil est minimale.
Comme pour les circonstances générales, on donne également les lieux de la surface terrestre ayant Vénus à son zénith au moment des contacts.
On donne également pour chaque contact, l’angle au pôle du contact, c’est l’angle entre le segment joignant le centre du Soleil et le point de contact sur le limbe solaire et la direction du nord céleste et compté positivement à partir du nord vers l’est (figure 1).
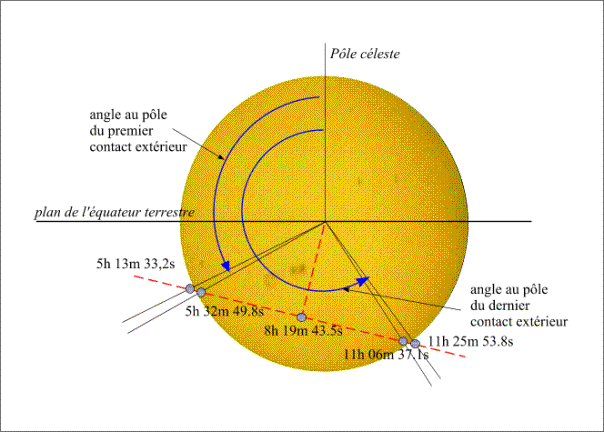
Figure 1. – Circonstances géocentriques.
|
Phases
géocentrique |
Instant en UTC |
Lieu ayant la planète au
zénith |
Angle au Pôle |
|
|
Longitude |
Latitude |
|||
|
Premier
contact extérieur |
5h 13m 33,2s |
-101° 37,9' |
+22° 45,3' |
+116° 15,7' |
|
Premier
contact intérieur |
5h 32m 49,8s |
- 96° 47,5' |
+22° 45,1' |
+119° 22,7' |
|
Maximum
du passage |
8h 19m 43,5s |
- 54° 52,6' |
+22° 43,1' |
--- |
|
Dernier
contact intérieur |
11h 6m 37,1s |
- 12° 57,8' |
+22° 41,0' |
+213° 13,2' |
|
Dernier
contact extérieur |
11h 25m 53,8s |
- 8° 7,3' |
+22° 40,8' |
+216° 20,2' |
Durées des phases géocentriques
Durée du passage général : 6h 12m 20,68s.
Durée du passage de l'ombre : 5h 33m 47,26s.
Distance angulaire géocentrique minimale : 10' 26,875".
Remarques
Les durées des phases géocentriques sont plus courtes que les durées des phases générales, cette différence correspond au temps que mettent les bords des cônes d’ombre et de pénombre pour parcourir un rayon terrestre.
La différence entre la distance angulaire géocentrique minimale et la distance angulaire topocentrique minimale correspond à la différence de parallaxe entre le centre de la Terre et un lieu voyant le minimum à l’horizon, donc les deux corps près de l’horizon. Cette différence doit donc être de l’ordre des différences des parallaxes horizontales équatoriales de Vénus et du Soleil. C’est bien le cas, on a 10' 26,875" – 10' 5,156" = 21,719" et la différence des parallaxes équatoriales vraies (au moment de la conjonction) est de 30,44" – 8,66" = 21,78".
IV. Les circonstances locales
Les circonstances locales sont en tous points semblables aux circonstances géocentriques mais elles se rapportent à un lieu particulier. Nous ne donnerons pas ici les circonstances locales pour de nombreux lieux à la surface de la Terre, par manque de place et aussi parce que nous ne voulons pas influencer les mesures que vous désirez faire. Nous donnons les valeurs, pour chaque contact, des coefficients E, F et G décrits dans les fiches précédentes. Ces coefficients permettent de calculer les valeurs approchées des contacts en un lieu quelconque à partir des instants des contacts géocentriques.
|
Phase |
E |
F |
G |
|
Premier contact extérieur |
6,4823min |
– 0,0556min |
2,8992min |
|
Premier contact intérieur |
6,6111min |
0,6731min |
3,3721min |
|
Dernier contact intérieur |
3,2893min |
3,4236min |
– 5,7456min |
|
Dernier contact extérieur |
2,8106min |
3,8404min |
– 5,2725min |
L’écart avec les instants des contacts géocentriques est donné par la formule suivante :
![]()
où l et j représentent les longitude et latitude du lieu d’observation.
Exemple : Calcul des circonstances locales pour Paris :
Les coordonnées géographiques de Paris sont les suivantes :
Latitude : 48° 50' 11,2" nord = 48.8364°
Longitude : –2° 20'13,8" (est) = –2.3372°
|
Contacts topocentriques |
Dt calculés à l’aide de la formule (1) |
Instant calculé à l’aide de la formule (1) |
Instants calculés à l’aide des formules exactes |
|
Premier contact extérieur |
6,4474min |
5h 20m 0,0s |
5h 20m 6,1s |
|
Premier contact intérieur |
6,8685min |
5h 39m 41,9s |
5h 39m 48,3s |
|
Dernier contact intérieur |
–2,2539min |
11h 4m 21,9s |
11h 4m 20,8s |
|
Dernier contact extérieur |
–2,2237min |
11h 23m 40,4s |
11h 23m 39,9s |
On constate que les écarts entre les valeurs approchées et les valeurs calculées avec les formules rigoureuses, donc sans approximation, sont bien de l’ordre du dixième de minute.
V. Les cartes de visibilité.
Ces cartes sont faites en utilisant la projection de Mercator. Cette projection classique en géographie, élaborée par Mercator en 1569, porte à tort le nom de projection, il s’agit en réalité d’un développement cylindrique conforme. Cette projection est bien adaptée à la navigation maritime car les routes à azimut constant sont représentées par des droites. Par contre elle présente l’inconvénient de dilater les latitudes au fur et à mesure que l’on s’éloigne de l’équateur. Les cercles ne sont donc pas représentés par des cercles mais par des courbes allongées vers les pôles.
Le tracé des cartes publiées a été fait à l’aide du logiciel GMT (Generic Mapping Tools Graphics) élaboré par Paul Wessel (School of Ocean and Earth Science and Technology, Universty of Hawaï at Manoa) et Walter. H. F. Smith (Laboratory for Satellite Altimetry, NOAA/NESDIS/NODC).
Nous donnons trois cartes :
Une carte de visibilité comportant les limites de visibilité du phénomène. Nous sommes proche du début de l’été, il existe donc une zone proche du pôle terrestre nord où le Soleil ne se couche pas, la totalité du passage est donc visible dans cette zone mais le Soleil est bas sur l’horizon. Inversement, proche du pôle terrestre sud, il existe une zone où le Soleil ne se lève pas, le passage y est donc invisible. On remarquera également deux zones, une au sud où le Soleil va se lever puis se recoucher et une au nord où le Soleil va se coucher puis se relever durant le passage.
La deuxième carte est identique à la première, mais comporte en plus trois types de courbes, les courbes de début et de fin du passage à un instant donné et les courbes d’égales durées du passage total. Les courbes début et fin à un instant donné sont les lieux sur Terre où les contacts extérieurs ont lieu à un même instant. Les courbes d’égales durées sont les lieux sur Terre où la totalité du passage, c’est-à-dire la différence de temps entre le dernier et le premier contacts extérieurs est égale. On remarque que ces courbes ne sont pas parallèles aux méridiens terrestre.
La troisième carte est identique à la seconde, mais, les courbes de début et de fin du passage à un instant donné et les courbes d’égales durées du passage correspondent aux contacts intérieurs et à la durée du passage intérieur.
Le phénomène que l’on va observer
Depuis un lieu quelconque de la zone de visibilité complète du phénomène, un observateur va assister au passage du disque de Vénus devant le disque solaire. La trajectoire apparente du passage de Vénus sur le disque va dépendre de deux choses :
§ Du lieu d’observation puisque l’on va exploiter la différence observée d’un lieu à l’autre pour déterminer la parallaxe.
§ Du repère dans lequel on se place pour observer. En effet, si l’on utilise un repère d’observation équatorial (lunette ou télescope sur une monture équatoriale suivant le Soleil dans son mouvement diurne) la trajectoire de Vénus sera quasi-rectiligne. Si par contre on utilise un repère d’observation azimutal (solarscope, vénuscope ou tout système de projection sur un écran fixe, donc fixe par rapport au zénith du lieu d’observation), la trajectoire de Vénus sera plus complexe.
C’est pourquoi on donne deux paramètres utiles à la détermination des points de contacts du passage :
L’angle au pôle « P » d’un contact est l’angle ayant pour sommet le centre du Soleil et pour cotés la direction du pôle nord céleste et la direction du contact. Il est compté positivement vers l’est à partir de la direction du pôle.
L’angle au zénith « Z » d’un contact est l’angle ayant pour sommet le centre du Soleil et pour cotés la direction du zénith du lieu et la direction du contact. Il est compté positivement vers l’est à partir de la direction du zénith.
On donne ci-dessous les circonstances locales et les trajectoires observables à Paris pour ces deux types d’observations.
Paris : latitude : 48°51'54.18" N; longitude : 2°20'59.16" E.
UT P Z
Premier contact extérieur : 5h 20m 6,0s 117,7° 159,8°
Premier contact intérieur : 5h 39m 48,2s 121,0° 164,2°
Dernier contact intérieur : 11h 4m 20,6s 212,4° 228,9°
Dernier contact extérieur : 11h 23m 39,7s 215,6° 225,4°
Durée de la phase centrale : 5h 24m 32.4s.
Durée de la phase générale : 6h 3m 33.7s.
Caractéristiques du maximum du passage :
Instant du maximum : 8h 22m 53.4s
Minimum de distance : 10' 40,9"
Hauteur du Soleil : 42°
Azimut du Soleil : 284°
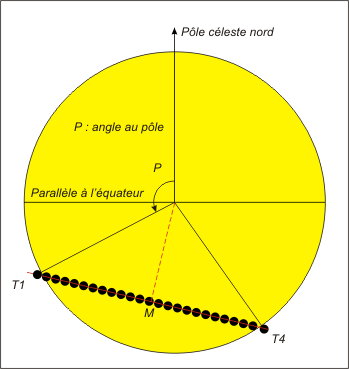
Figure 2. – Aspect du passage de Vénus à Paris dans
le repère équatorial
par exemple vue à l’aide d’une lunette munie d’une monture équatoriale.
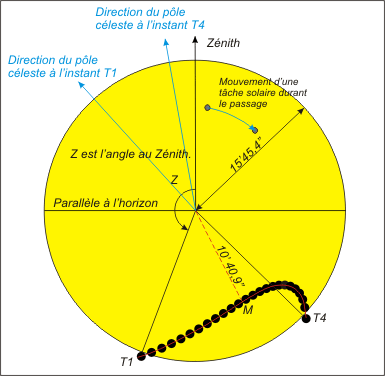
Figure 3. –
Aspect du passage de Vénus à Paris dans
le repère horizontal par exemple vue à l’aide d’un solarscope.
On constate que la mesure du minimum de distance dans le cas d’une trajectoire rectiligne est beaucoup plus « facile » que la mesure du minimum de distance dans le cas d’un trajectoire curviligne.