Fiche pédagogique n° 04b :
Calcul de la parallaxe à partir des observations

P. Rocher(IMCCE)

I. Introduction

Nous avons vu que les passages de Vénus sont rares ; ils suivent depuis la fin du XVI^e siècle le cycle 105.5 ans, 8 ans, 121.5 ans et 8 ans. Plus d’un siècle sépare donc un couple de passages espacés de huit ans. Durant ces siècles les méthodes d’observation et la technologie ont évolué fortement.

Au XVIII^e siècle les éphémérides des astres étaient d’assez faible précision, on ne savait pas bien mesurer la longitude d’un lieu et il n’existait pas d’horloges vraiment fiables.

Au XIX^e siècle, les éphémérides avaient progressé en précision ; la détermination précise de la longitude, surtout pour des lieux très éloignés non reliés par des télégraphes, posait encore quelques problèmes et en ce qui concerne le transport du temps, les horloges avaient fait de gros progrès. Un nouveau moyen d’observation avait fait son apparition : la photographie.

De nos jours tous ces problèmes n’existent plus. Les positions sur Terre sont directement accessibles à l’aide du GPS. Le temps universel est disponible en tout point du globe avec une précision surabondante. Les méthodes d’observation et d’enregistrement sont à la fois nombreuses et variées. On pourrait donc s’attendre à une amélioration de la connaissance de la valeur de la parallaxe solaire à l’aide de l’observation des passages de Vénus. En réalité, ce ne sera pas le cas, car dans le même temps des méthodes directes de mesure de distances sont apparues et leurs précisions sont supérieures à toutes les autres méthodes même pourvues des dernières technologies. La parallaxe solaire est connue de nos jours à 10^-6 seconde de degré près.

Néanmoins le passage de Vénus sera très intéressant à observer et à enregistrer, et il sera possible comme pour les passages intérieurs d’en déduire des valeurs de la parallaxe, même si c’est dans un but purement pédagogique.

On va voir que l’on peut faire plusieurs types de mesures qui auront des méthodes de réductions assez semblables.

II. Problème lié au temps d’observation

Lors des passages précédents les observations temporelles devaient être ramenées au temps moyen de Paris (ou de Greenwich). L’observation était faite avec une horloge calée sur le temps solaire moyen du lieu, ce temps solaire moyen local était lui-même déduit du temps sidéral local observé grâce aux passages au méridien des étoiles et du Soleil. Ensuite les instants d’observation en temps solaire moyen étaient transformés en temps moyen de Paris (ou de Greenwich) en ajoutant ou en retranchant la longitude du lieu. Une erreur en longitude se reportait donc directement sur le temps d’observation obtenu, d’où l’intérêt de la méthode de Halley qui, en mesurant la durée du phénomène, faisait disparaître la longitude des équations.

La méthode de Delisle qui consistait à comparer les instants d’observations de deux contacts identiques, exprimés en temps moyens locaux, ne supprimait pas le terme en longitude et nécessitait donc une bonne connaissance de cette dernière. Mais elle avait l’avantage de pouvoir être utilisée sur une plus grande partie du globe terrestre, l’observation globale du phénomène n’étant plus nécessaire. De nos jours les instants sont directement mesurés en temps universel, ou dans une échelle de temps décalée d’un nombre entier d’heures par rapport au temps universel, les éventuelles erreurs en longitude n’apparaissent plus que dans les termes en sinus et en cosinus de la longitude.

Malgré cela nous garderons dans les expressions que nous allons calculer le terme en dl représentant l’erreur due à la longitude, car il est intéressant de voir comment il intervenait dans la réduction des observations par le passé. Chaque observation est également entachée d’incertitudes que l’on arrive à moyenner en utilisant un grand nombre d’observations ou en combinant judicieusement certaines d’entres elles.

Dans les méthodes de réduction présentées dans les paragraphes suivants, on utilise des valeurs calculées des quantités mesurées. Pour cela on utilise une estimation de la parallaxe équatoriale moyenne solaire p₀ et c’est cette estimation que l’on va améliorer en comparant les valeurs calculées et les valeurs mesurées. Les valeurs calculées doivent être calculées avec le maximum de précision possible, des valeurs approchées peuvent être utilisées dans un but pédagogique, mais les erreurs qu’elles génèrent risquent d’être trop fortes pour certains types de mesure.

Dans les formules que nous avons développées, nous allons négliger l’aplatissement de la Terre. Pour tenir compte de l’aplatissement terrestre f et de la hauteur h de l’observateur, il suffira de remplacer dans ces formules le cosinus et le sinus de la latitude géographique j par le cosinus et le sinus de la latitude géocentrique j' et de multiplier les coordonnées cartésiennes géographiques par r exprimé en rayon terrestre. On rappelle que l’on passe de la latitude géographique à la latitude géocentrique à l’aide des formules suivantes :

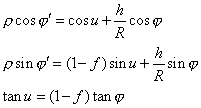
III. Mesures de distance et de temps.

Premier type de mesure

On mesure la projection de la distance des centres de Vénus et du Soleil sur la tangente au parallèle céleste passant par le centre du Soleil.

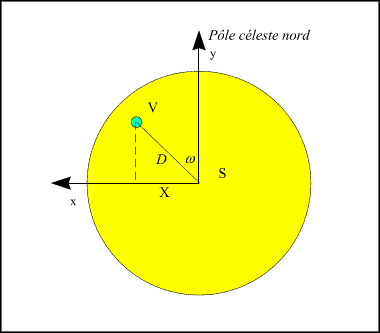
Figure 1. – Mesure de la projection X de la distance.

Nous avons nommé cette quantité X dans les explications précédentes (figure 1).

Soit X la valeur pour un observateur situé au centre de la Terre et soit X_p la valeur pour un observateur à la surface de la Terre. Nommons X_o la quantité observée et X_c la quantité calculée.

La valeur de X_p se déduit de la valeur de X par la formule suivante (cf. formule 12 de la fiche II= :

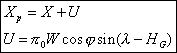
U est la parallaxe sur X en coordonnées différentielles tangentielles, j et l sont les coordonnées géographiques de l’observateur et H_G est l’angle horaire de Soleil au méridien de Greenwich à l’instant de l’observation. W est la différence des inverses des distances Soleil-Terre et Soleil-Vénus.

Si l’on nomme dl l’erreur en longitude, dx l’erreur sur le calcul de X due aux éphémérides, DX_o l’incertitude de mesure de la quantité X_o, Dt l’incertitude de mesure du temps d’observation et dp₀ la correction à apporter à p₀, alors l’équation de condition reliant la valeur observée et la valeur calculée est la suivante :

Si l’on développe le sinus dans l’expression de U, cette équation s’écrit :

Dans cette équation les termes j = –W.sin H_G, k = W.cos H_G et dX/dt ne dépendent pas du lieu d’observation et peuvent être calculés et tabulés par avance. Le terme dx peut être considéré comme constant sur la durée du passage.

Dans ces équations Dt et DX₀ sont les incertitudes les mesures et les trois inconnues sont dp₀ , dx et dl. La résolution de cette équation linéaire à trois inconnues demande la connaissance d’au moins trois observations. Si l’on a plus de trois observations, le système peut être résolu par des méthodes statistiques (méthode des moindres carrés). L’usage d’un grand nombre d’observation permet de moyenner les incertitudes sur les observations Dt et DX_o.

Si l’on considère les éphémérides comme parfaites et si l’on suppose la longitude parfaitement connue alors l’équation n’a plus qu’une inconnue :

Remarquons que les unités utilisées doivent être homogènes, le coefficient de dp₀ est sans dimension, si X_o et X sont en secondes de degré alors dp₀ sera dans la même unité et si dX/dt est en secondes de degré par minute de temps alors Dt doit également être en minutes de temps.

On remarquera dans ces équations que les termes cosj cosl et –cosj sinl sont respectivement les coordonnées cartésiennes de l’observateur dans le plan de l’équateur, l’axe Ox étant la direction du méridien de Greenwich.

Deuxième type de mesure

On mesure la projection de la distance des centres de Vénus et du Soleil sur la tangente au méridien céleste passant par le centre du Soleil.

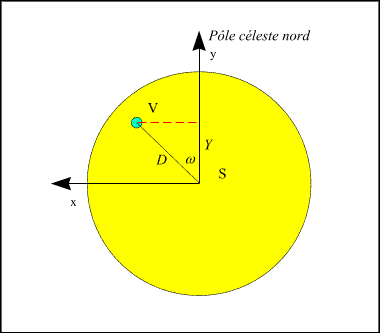
Figure 2. – Mesure de la projection Y de la distance.

Nous avons nommé cette quantité Y dans les explications précédentes (figure 2).

Soit Y la valeur pour un observateur situé au centre de la Terre et soit Y_p la valeur pour un observateur à la surface de la Terre. Nommons Y_o la quantité observée et Y_c la quantité calculée.

La valeur de Y_p se déduit de la valeur de Y par la formule suivante (cf. formule 12 de la fiche II) :

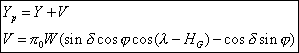
V est la parallaxe sur Y en coordonnées différentielles tangentielles.

Si l’on nomme dl l’erreur en longitude, dy l’erreur sur le calcul de Y due aux éphémérides Dt l’incertitude de mesure du temps, DY_o l’incertitude de mesure sur Y_o et dp₀ la correction à apporter à p₀, alors l’équation de condition reliant la valeur observée et la valeur calculée est la suivante :

Si l’on développe le cosinus dans l’expression de V cette équation s’écrit :

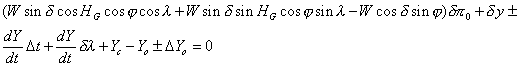
Dans cette équation les termes l = Wsind cosH_G, m = Wsind sinH_G, n = –W cosd et dY/dt ne dépendent pas du lieu d’observation et peuvent être calculés et tabulés par avance. Le terme dy peut être considéré comme constant sur la durée du passage.

La résolution de cette équation linéaire à trois inconnues demande la connaissance de trois observations. Si l’on a plus de trois observations, le système peut être résolu par la méthode des moindres carrés.

Si l’on considère les éphémérides comme parfaites et si l’on suppose la longitude parfaitement connue alors l’équation n’a plus qu’une inconnue :

On remarquera dans ces équations que les termes cosj.cosl, –cosj.sinl et sinj sont respectivement les coordonnées cartésiennes de l’observateur dans le repère cartésien équatorial défini par le méridien de Greenwich et l’équateur terrestre.

Troisième type de mesure

On mesure la projection de la distance des centres de Vénus et du Soleil sur un rayon du disque solaire de direction connue.

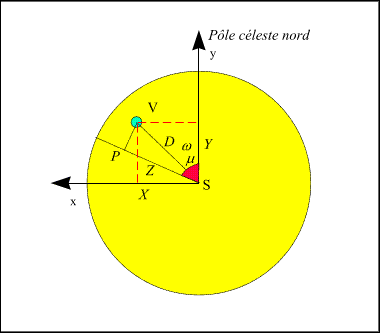
Figure 3. – Mesure de la projection de la distance sur un rayon quelconque.

Soit SP la projection de SV sur le rayon solaire de direction m par rapport au pôle céleste nord compté positivement vers l’est (figure 3).

Soit Z la valeur pour un observateur situé au centre de la Terre et soit Z_p la valeur pour un observateur à la surface de la Terre. Nommons Z_o la quantité observée et Z_c la quantité calculée. De nouveau Dt est l’incertitude sur la mesure du temps et DZ_o est l’incertitude sur la mesure de Z

La valeur de Z_p se déduit de la valeur de Z par les formules suivantes :

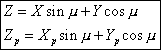
Et en utilisant les formules introduites dans les deux cas précédents on a :

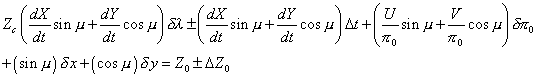
Ce qui donne en introduisant les paramètres j, l, k, m et n l’équation de condition suivante :

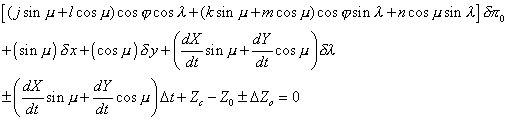
Cette formulation est à utiliser notamment lorsque l’on projette la distance entre les centres sur la verticale du lieu contenant le centre du Soleil (par exemple sur une observation faite avec une lunette ayant une monture horizontale), dans ce cas m est l’opposé de l’angle à l’astre S du Soleil. L’angle à l’astre est l’angle formé par la direction joignant le centre du Soleil au zénith et la direction joignant le centre du Soleil au pôle céleste nord et compté positivement vers l’ouest à partir du vertical contenant le centre du Soleil (figure 4).

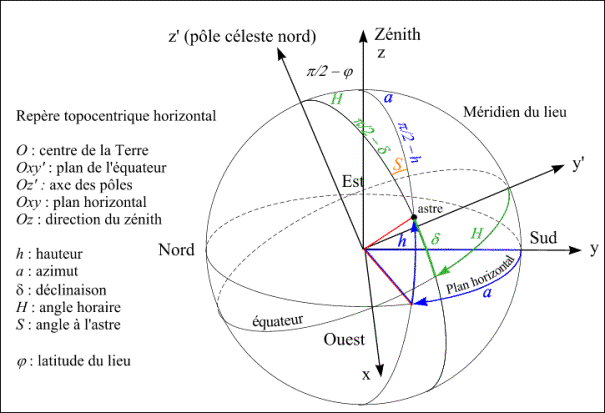
Figure 4. –.La sphère céleste horizontale locale.

Quatrième type de mesure

On mesure la distance angulaire des centres de Vénus et du Soleil.

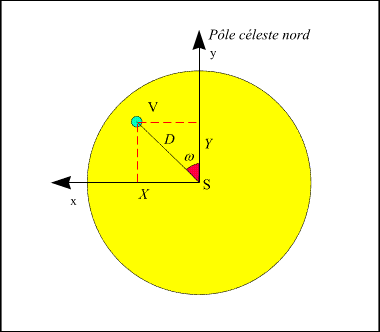
Figure 5. – Mesure de la distance des centres des deux astres.

Nous avons nommé cette quantité D dans les explications précédentes (figure 5).

Soit D la valeur pour un observateur situé au centre de la Terre et soit D_p la valeur pour un observateur à la surface de la Terre. Nommons D_o la quantité observée et D_c la quantité calculée. Soit DD_o l’incertitude sur la mesure de D_o et Dt l’incertitude sur le temps mesuré.

La valeur de D_p se déduit de la valeur de D par les formules suivantes :

et (cf. formule 6 de la fiche II)

dans cette équation les coefficients a, b et c sont indépendants du lieu.

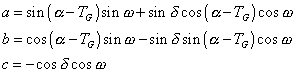
On en déduit l’équation de condition suivante :

Si l’on introduit les paramètres suivants : A = Wa, B = Wb et C = Wc alors l’équation de condition devient :

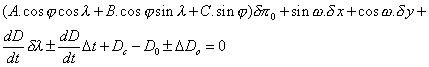
Les quantités A, B, C, sinw, cosw, dD/dt ne dépendent pas de l’observateur et peuvent être calculées et tabulées à l’avance.

On remarque également que le terme contenant l’erreur sur la longitude a dD/dt en facteur, on avait donc intérêt lorsque cette longitude n’était pas bien déterminée à privilégier les observation près du minimum de distance, où dD/dt est proche de zéro, ou bien de combiner des observations symétriques par rapport à ce minimum pour supprimer ce terme.

Si les erreurs de calcul sur les valeurs de X et Y sont nulles et que l’erreur sur la longitude est également nulle, alors l’équation précédente devient :

De nouveau on constate que pour les valeurs proches du minimum l’effet de l’incertitude Dt sur le résultat sera quasi-nulle.

IV. Mesures de temps uniquement.

Les mesures précédentes, pour obtenir les valeurs calculées, demandaient la connaissance des instants d’observation. Dans ce chapitre nous allons traiter de mesures portant uniquement sur le temps. Ces mesures sont celles des instants des contacts extérieurs ou intérieurs et des durées de passages.

Observation d’un instant de contact.

Soit t_o l’instant observé d’un contact intérieur ou extérieur et soit t_c l’instant calculé avec la meilleure précision possible. On désigne par dd et dd' les corrections éventuelles que l’on a sur les demi-diamètres apparents du Soleil et de Vénus. On nomme D_c, d_c et d'_c les valeurs calculées de la distance angulaire entre les centres et des demi-diamètres des deux astres. Ces trois quantités doivent vérifier l’équation suivante :

Dans le passé la valeur t_o observée était entachée d’une erreur dl sur la longitude et l’heure véritable du contact était : t_o ± dl. De nos jours cette erreur n’existe pas car on mesure directement l’instant du contact en temps universel. Nous la garderons malgré tout dans nos formules pour comprendre l’intérêt des méthodes utilisées aux passages précédents. Nous noterons Dt l’incertitude sur la mesure de l’instant du contact.

Le premier membre de l’équation précédente devient la distance vraie entre les centres si on lui ajoute la correction suivante :

Et l’on doit ajouter au second membre les erreurs sur les demi-diamètres. Ce qui donne :

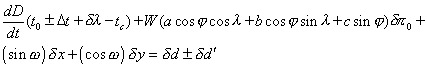
ou encore en introduisant les paramètres A, B et C :

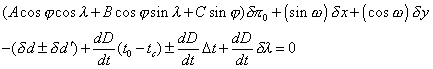
De nouveau les quantités A, B, C, sinw, cosw et dD/dt sont indépendantes de l’observateur et peuvent être calculées à l’avance.

Cette équation de condition compare une valeur mesurée à une valeur calculée, on peut comparer deux valeurs mesurées d’un même contact (méthode de Delisle), si l’on affecte de l’indice 1 l’équation de condition de la première observation et d’un indice 2 l’équation de condition de la seconde observation, ces équations s’écrivent :

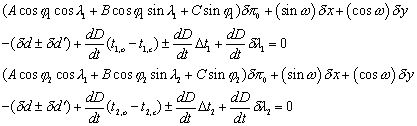
et la différence des deux équations donne :

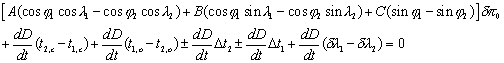
Comme on le voit une partie des erreurs disparaissent, il ne subsiste plus que l’erreur en longitude, qui est multipliée par le même facteur que les mesures temporelles. D’où l’importance d’avoir une bonne détermination des longitudes pour appliquer la méthode de Delisle.

Il convient de faire une remarque sur cette dernière équation, elle contient encore la différence des instants des contacts calculés. On pourrait être tenté de remplacer cette expression par sa formulation simplifiée (établie dans la ficher « Comment calculer les circonstances d’un passage de Vénus devant le Soleil) qui est égale à :

alors on aurait directement une estimation de la nouvelle valeur de la parallaxe p₀ +dp₀ mais ce serait une erreur, en effet les valeurs approchées du calcul des contacts sont faites avec une erreur de l’ordre du dixième de minute, en prenant ces valeurs simplifiées on intègre cette erreur dans la valeur de la parallaxe ; il convient donc de garder dans les formules les valeurs des contacts calculées avec le maximum de précision. Si l’on utilise cette simplification la formule (15) devient :

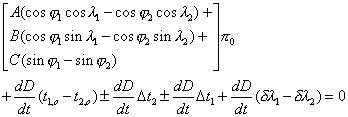
Cette formule simplifiée permet d’avoir une première approximation de la parallaxe.

On remarque également que la combinaison des lieux d’observation doit être faite de sorte que la différence des temps de contacts soit maximale.

Observation de la durée d’un passage.

L’étude et la détermination de l’équation de condition liée à la durée d’un passage sont en tous points identiques à l’études des contacts, on fait simplement la différence de deux contacts identiques pour un même lieu. Par exemple pour la durée du passage intérieur on utilise le deuxième et le troisième contacts notés 2 et 3 on obtient en ajoutant les deux équations :

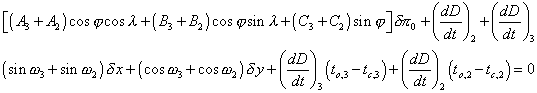
Or pour des raison de symétrie on a :

L’équation précédente se met alors sous la forme :

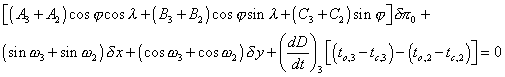
On constate que le terme en longitude a disparu, d’où l’intérêt de cette méthode lorsque l’on ne pouvait pas bien déterminer les longitudes des observateurs.

Si l’on nomme T_o la durée observée et T_c la durée calculée, l’équation précédente devient :

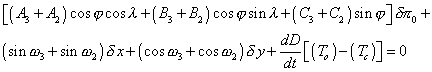
Maintenant si on utilise la méthode de Halley en deux points a et b et si l’on nomme DT_o la différence de temps de passage observée et DT_c la différence de temps de passage calculée, on a l’équation de condition suivante :

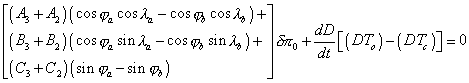
Les termes correspondant aux erreurs de tables ont disparu des équations.

On voit que l’on a intérêt à avoir une valeur extrême pour le différence des durées observées DT₀. En effet il faut que l’écart de durée entre les points a et b soit le plus grand possible devant l’écart entre la valeur mesurée et la valeur calculée.

Remarque : si l’on ne connaît pas d’estimation de p₀ l’équation (12) de la fiche III dans laquelle on fait apparaître les coefficients A, B, et C permet d’écrire :

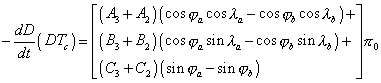
Et finalement :

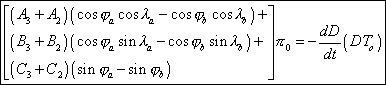
Cette dernière formule permet donc de calculer directement la parallaxe à l’aide de deux observations de durée, par contre l’usage de l’équation (20) introduit des erreurs du dixième de minutes de temps sur les contacts, donc sur les durées calculées. Cette formule est donc à utiliser pour avoir une première approximation de la parallaxe mais pas pour réduire des séries observations.

Remarques

À la fin du XIX^e siècle, après les passages de 1874 et 1882, les réductions des observations obtenues à l’aide de clichés photographiques utilisèrent des équations de condition légèrement différentes de celles élaborées ci-dessus. La comparaison des observations de distances entre les centres des deux corps avec les distances calculées ne laissa aucun doute sur l’existence d’une erreur personnelle liée à chaque observateur. Cette comparaison indiqua également que la somme des rayons des deux astres admise à l’époque était trop forte d’environ 3", en raison notamment de la diffraction. On introduisit donc deux nouvelles inconnues, l’équation personnelle et l’erreur sur la somme des rayons. Ces deux nouvelles inconnues se réduisaient à une seule si l’on regroupait les résultats de chaque observateur.

Le résultat de la mesure était le rapport de la distance des centres sur la somme des rayons des deux astres. Soit m ce rapport, D la distance des centres, S la somme des rayons et e l’erreur personnelle. On a :

donc

Or seule dm est entachée d’une erreur personnelle. Donc :

Et enfin

en posant

l’équation de condition sur la distance D devient alors :

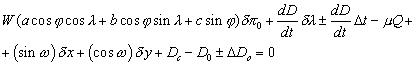
D’autre part, la réduction des observations obtenues à l’aide de clichés photographiques a amené une nouvelle méthode de réduction basée sur le tracé de la trajectoire du centre de Vénus devant le Soleil. Cette trajectoire est représentée par une hyperbole, la connaissance de cette hyperbole permet de connaître la distance minimale entre les centres. On pratique toujours de la même manière, on calcule la trajectoire géocentrique, puis la trajectoire topocentrique et l’on mesure la trajectoire sur les clichés. On détermine alors une équation de condition qui ne dépend plus que de trois paramètres. On détermine par une méthode de moindres carrés ces trois paramètres, puis on obtient la correction de parallaxe en comparant les valeurs obtenues dans les différentes stations d’observations. Cette méthode plus complexe ne sera pas détaillée dans ce document.