Fiche pédagogique n° 04c :
Exemples de calcul de la parallaxe à partir des
observations.
(avec les données pour la réduction des observations)
P. Rocher (IMCCE)
I.Introduction
Nous allons donner une série d’exemples de calcul de la valeur de la parallaxe à l’aide des formules que nous avons développées précédemment.
Nous allons nous placer à l’observatoire de Paris dont les coordonnées sont les suivantes :
j = 48° 50' 11,2" nord, l = 2° 20' 13,8"est (9min 20,92s est) et h = 67m.
Le rayon terrestre R est égal à : 6378,140 km
Nous allons tenir compte de l’aplatissement terrestre f = 1/298,257.
En utilisant les formules suivantes on peut déterminer la latitude géocentrique j' et le facteur r.
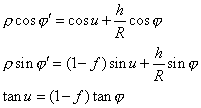
j' = 48° 38' 44,38" et r = 0,9981171849.
r sinj' = 0,7492245345 et r cosj' = 0,6594698717.
La parallaxe équatoriale solaire p0 = 8,79414".
Exemple 1
Mesure de la projection de la distance des centres de Vénus et du Soleil sur la tangente au parallèle céleste passant par le centre du Soleil.
Nous avons noté Xo cette valeur.
Pour simplifier les calculs et éviter les interpolations des tables, nous allons choisir un instant de la tabulation pour notre exemple : 6h 5m UTC.
Nous allons calculer une valeur approchée Xc de Xp pour l’instant d’observation à l’aide de la formule (cf. formule 2 fiche VI) :
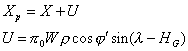
où l’on peut développer le sinus et faire apparaître les paramètres j et
k (j = –W.sin
HG, k = W.cos HG).
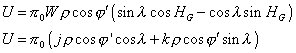
Les tableaux de données nous fournissent les valeurs suivantes :
X = 11,2181', j = 2,4756 et k = 0,0644.
Ce qui donne U = 0,2388' et Xc = 11,4569'.
Le calcul rigoureux, sans approximation, donne Xc = 11,4574'
soit une différence de 0,03".
Supposons que l’on observe par projection et que le disque solaire ait un rayon de 10 cm. Le demi-diamètre apparent du Soleil étant de l’ordre de 945,4" la projection d’une seconde de degré mesure 0,106mm et le rayon de la projection de Vénus mesure environ 3mm. On se rend compte de la difficulté de réaliser une mesure précise. Supposons que vous mesuriez une projection Xo au centre du Soleil égale à 7,28 cm avec une précision du demi-millimètre (0,05 cm), ce qui donne une mesure en minute de degré égale à Xo = 11,4708' avec une incertitude de DXo = 4,727" = 0,0788'.
Pour réduire cette observation nous allons utiliser la formule suivante (cf. formule 4 fiche VI) :
![]()
le coefficient de dp0 est égal à 1,6295 et dX/dt est égal à –3,9166"/min.
La différence de la valeur observée et de la valeur calculée est de –0,0134' (–0,8072"), si l’on exprime tout en secondes de degré nous trouvons :
![]()
Ce qui donne pour la parallaxe équatoriale moyenne :
![]()
Cet exemple montre l’importance
de la précision dans la mesure de X et l’influence de la précision du
temps d’observation. Le demi-millimètre de précision dans la mesure de X
produit des incertitudes de l’ordre de trois secondes de degré sur la valeur de
la parallaxe ! Alors qu’une erreur d’une seconde sur l’instant
d’observation ne produit qu’une incertitude de 0,04" sur la valeur de la
parallaxe.
Exemple 2
Mesure de la projection de la distance des centres de Vénus et du Soleil sur la tangente au méridien céleste passant par le centre du Soleil.
Nous avons noté Yo cette valeur.
Pour simplifier les calculs et éviter les interpolations des tables, nous allons choisir le même instant de la tabulation pour notre exemple : 6h 5m UTC.
Nous allons calculer une valeur approchée Yc de Yp pour l’instant d’observation à l’aide de la formule (cf. formule 5 fiche VI) :
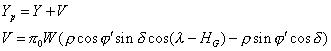
où l’on peut développer le cosinus et faire apparaître les paramètres l, m et n (l = Wsind cosHG, m = Wsind sinHG, n = –W cosd)
![]()
Les tableaux de données nous fournissent les valeurs suivantes :
Y = -8,0142', l = 0,0251, m = –0,9625 et n = –2,2816.
Ce qui donne U = –0.2443' et Yc = –8.2585'.
Le calcul exact sans approximation donne Yc = –8,2590' soit une différence de 0,03".
Supposons que l’on observe de nouveau par projection et que le disque solaire ait un rayon de 10 cm. Supposons que vous mesuriez une projection Yo au centre du Soleil égale à –5,25 cm avec une précision du demi-millimètre (0,05 cm), ce qui donne une mesure en minute de degré égale à Yo = -8,2723' avec une incertitude de DYo = 4,727" = 0,0788'.
Pour réduire cette observation nous allons utiliser la formule suivante (cf. formule 7 fiche VI) :
![]()
Le coefficient de dp0 est égal à –1,6670 et dY/dt est égal à –0,9595"/min, ce qui donne en convertissant tout en secondes de degré :
![]()
On constate de nouveau l’importance de l’erreur introduite par l’incertitude de la mesure de Y.
Exemple 3
Mesure de la distance angulaire entre les centres de Vénus et du Soleil.
Nous avons noté Do cette valeur.
Nous utilisons toujours le même instant t=6h 05m.
Nous pouvons calculer une valeur approchée Dc de Dp par la formule suivante (cf. formule 11 fiche VI) :
![]()
Pour l’instant les tableaux de données fournissent :
D = 13,7867', A = 1,9998, B
= 0,6119, C = 1,3263.
Ce qui donne Dc = 14,1231', le calcul rigoureux, sans approximation donne 14,1239', soit un écart de 0,048".
Supposons que l’on observe de nouveau par projection et que le disque solaire ait un rayon de 10 cm. Supposons que vous mesuriez une projection Do au centre du Soleil égale à 8,97 cm avec une précision du demi-millimètre (0,05 cm), ce qui donne une mesure en minute de degré égale à Do = 14,1337' avec une incertitude de DYo = 4,727" = 0,0788'.
Pour réduire cette observation nous allons utiliser la formule suivante (cf. formule 13 fiche VI) :
![]()
Le coefficient de dp0 est égal à 2,2949 et dD/dt est égal à –2,6290"/min, ce qui donne en convertissant tout en secondes de degré :
![]()
De nouveau on constate l’importance de l’incertitude de la mesure sur D.
Commentaires historiques
Quelles étaient ces valeurs pour les observations du XIXe siècle ?
L’observation photographique à l’île St-Paul en 1874.
Les plaques (110mm x 68mm) prises à l’île St-Paul par l’équipe du
commandant Mouchez, produisaient une image du Soleil de l’ordre de 31mm, les
mesures faites donnent le rapport suivant 1mm sur les clichés correspond à
54,4974" dans le sens horizontal et 54,402" dans le sens horizontal,
les instants des clichés étaient donnés au dixième de seconde de temps. La
lunette photographique avait un objectif de 135 millimètres d’ouverture et une
distance focale de 3,80m, l’image du Soleil était projetée sur la plaque
photographique qui se trouvait à 43mm de l’objectif. Les instants de prise de
vue étaient enregistrés à l’aide d’un chronographe électrique couplé à une
pendule sidérale. Au total les observateurs de l’île St-Paul ramenèrent 124
plaques daguerriennes représentant 443 poses, et 47 plaques au collodion
représentant 142 poses (on effectuait plusieurs poses par plaques).
La réduction des plaques du passage de 1882.
Les mesures des 1019 plaques des passages de 1882 ont été faites de la
manière suivante : les clichés étaient agrandis en même temps qu’un réseau
de fils. Le réseau de fils avait pour but de mesurer les déformations des
plaques, puis le bord du Soleil était pointé 64 fois et le bord de Vénus était
pointé 24 fois, ces pointages étaient faits à l’aide de microscopes et la
précision était de l’ordre du micron. On déduisait de ces pointés les centres
des deux astres et leurs distances. On obtint finalement 900 valeurs des
différences entre les valeurs mesurées et les valeurs calculées réparties sur
cinq sites d’observation. Les mesures faites deux fois et par deux personnes à
chaque fois correspondent à environ 400000 pointés et 500000 lectures aux
micromètres et aux échelles ; l’ensemble des mesures prit plus de quinze
mois !
Exemple 4
Mesure des instants des contacts intérieurs.
Par exemple le premier contact intérieur à l’observatoire de Paris.
Nous avons vu que l’équation de condition pour un contact peut s’écrire
sous la forme suivante (cf. formule 13 fiche VI) :
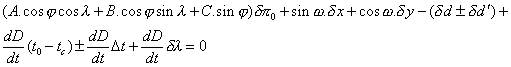
On peut supposer de nos jours que l’erreur des tables et l’erreur en longitude sont nulles.
L’équation devient alors :
![]()
Pour le premier contact intérieur les tableaux de données nous fournissent les valeurs suivantes :
A = 2,1970, B = 0,2237, C = 1,1206, dD/dt = –2,9394"/min.
Le calcul approché de ce contact donne tc = 5h 39m 41,9s et le calcul rigoureux donne tc = 5h 39m 48,3s, l’écart est de plusieurs secondes, il convient donc d’utiliser le calcul rigoureux dans la formule de réduction.
Le coefficient du terme dp0 est égal à : 2,2812.
Supposons que l’on mesure l’instant du contact to = 5h 39m 40s.
On a alors l’équation :
![]()
Ce qui donne :
![]()
Les erreurs sur les demi-diamètres sont exprimées en secondes de degré.
On peut faire un calcul identique pour le dernier contact extérieur.
A = –1,0929, B = –1,1376, C = 1,9090, dD/dt = 2,9391"/min.
Le calcul approché de ce contact donne tc = 11h 4m 21,9s
et le calcul rigoureux donne tc = 11h 4m 20,8s, l’écart n’est que de
l’ordre d’une seconde, on utilise malgré tout le calcul rigoureux dans la
formule de réduction.
Le coefficient du terme dp0 est égal à : 0,74073.
Supposons que l’on mesure l’instant du contact to = 11h 4m 18s.
On a alors l’équation :
![]()
Ce qui donne :
![]()
On peut faire plusieurs remarques sur les valeurs obtenues :
L’erreur de mesure, qui ne porte plus que sur le temps du contact, a un effet sur le résultat bien inférieur aux erreurs de mesure des distances des exemples précédents, néanmoins si l’on désire avoir une précision de l’ordre du centième de seconde de degré avec une seule observation l’erreur en Dt doit être de l’ordre de la seconde de temps.
La mesure de la durée du phénomène s’obtient en faisant la différence des deux équations 8 et 9, on obtient alors une équation où le terme lié aux demi- diamètres disparaît :
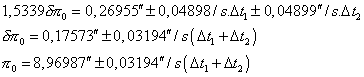
La combinaison des deux équations 8 et 9 permet également de calculer la
précision sur la différence des demi-diamètres.
L’usage d’un grand nombre d’observations et la méthode des moindres carrés
permettent de trouver les valeurs des deux inconnues (la correction de
parallaxe et l’erreur sur la différence des demi-diamètres).
Valeurs des paramètres pour le passage du 8 juin 2004
Les deux tableaux suivants donnent les valeurs des paramètres j, k, l, m, n, dX/dt, dY/dt, cosw et sinw avec un pas de tabulation de 5 minutes de temps. Toutes les valeurs sont sans dimension à l’exception de dX/dt et de dY/dt qui sont exprimées en secondes de degré par minute de temps.
|
T UTC |
j |
k |
l |
m |
n |
dX/dt "/min |
dY/dt "/min |
cosw |
sinw |
|
5h05m |
2.4080 |
-0.5784 |
-0.2248 |
-0.9360 |
-2.2817 |
-3.9161 |
-0.9621 |
-0.4232 |
0.9060 |
|
5h10m |
2.4200 |
-0.5258 |
-0.2044 |
-0.9407 |
-2.2817 |
-3.9161 |
-0.9619 |
-0.4347 |
0.9006 |
|
5h15m |
2.4309 |
-0.4728 |
-0.1838 |
-0.9450 |
-2.2817 |
-3.9162 |
-0.9617 |
-0.4466 |
0.8948 |
|
5h20m |
2.4406 |
-0.4197 |
-0.1632 |
-0.9488 |
-2.2817 |
-3.9162 |
-0.9615 |
-0.4587 |
0.8886 |
|
5h25m |
2.4492 |
-0.3664 |
-0.1424 |
-0.9521 |
-2.2817 |
-3.9163 |
-0.9613 |
-0.4711 |
0.8821 |
|
5h30m |
2.4566 |
-0.3129 |
-0.1216 |
-0.9550 |
-2.2817 |
-3.9163 |
-0.9611 |
-0.4838 |
0.8752 |
|
5h35m |
2.4629 |
-0.2592 |
-0.1008 |
-0.9575 |
-2.2817 |
-3.9163 |
-0.9609 |
-0.4968 |
0.8678 |
|
5h40m |
2.4679 |
-0.2054 |
-0.0799 |
-0.9594 |
-2.2817 |
-3.9164 |
-0.9607 |
-0.5102 |
0.8601 |
|
5h45m |
2.4718 |
-0.1515 |
-0.0589 |
-0.9610 |
-2.2816 |
-3.9164 |
-0.9605 |
-0.5238 |
0.8518 |
|
5h50m |
2.4745 |
-0.0976 |
-0.0379 |
-0.9620 |
-2.2816 |
-3.9165 |
-0.9604 |
-0.5377 |
0.8431 |
|
5h55m |
2.4761 |
-0.0436 |
-0.0170 |
-0.9626 |
-2.2816 |
-3.9165 |
-0.9602 |
-0.5520 |
0.8339 |
|
6h00m |
2.4764 |
0.0104 |
0.0041 |
-0.9628 |
-2.2816 |
-3.9166 |
-0.9600 |
-0.5665 |
0.8241 |
|
6h05m |
2.4756 |
0.0644 |
0.0251 |
-0.9625 |
-2.2816 |
-3.9166 |
-0.9598 |
-0.5813 |
0.8137 |
|
6h10m |
2.4736 |
0.1184 |
0.0460 |
-0.9617 |
-2.2816 |
-3.9167 |
-0.9596 |
-0.5964 |
0.8027 |
|
6h15m |
2.4705 |
0.1723 |
0.0670 |
-0.9605 |
-2.2816 |
-3.9167 |
-0.9594 |
-0.6117 |
0.7911 |
|
6h20m |
2.4661 |
0.2262 |
0.0879 |
-0.9588 |
-2.2816 |
-3.9167 |
-0.9592 |
-0.6273 |
0.7788 |
|
6h25m |
2.4606 |
0.2799 |
0.1088 |
-0.9567 |
-2.2816 |
-3.9168 |
-0.9590 |
-0.6432 |
0.7657 |
|
6h30m |
2.4539 |
0.3335 |
0.1297 |
-0.9541 |
-2.2816 |
-3.9168 |
-0.9588 |
-0.6592 |
0.7520 |
|
6h35m |
2.4460 |
0.3870 |
0.1505 |
-0.9511 |
-2.2816 |
-3.9169 |
-0.9586 |
-0.6754 |
0.7375 |
|
6h40m |
2.4370 |
0.4402 |
0.1712 |
-0.9476 |
-2.2816 |
-3.9169 |
-0.9584 |
-0.6918 |
0.7221 |
|
6h45m |
2.4268 |
0.4933 |
0.1918 |
-0.9436 |
-2.2816 |
-3.9170 |
-0.9582 |
-0.7082 |
0.7060 |
|
6h50m |
2.4155 |
0.5461 |
0.2123 |
-0.9392 |
-2.2816 |
-3.9170 |
-0.9580 |
-0.7248 |
0.6890 |
|
6h55m |
2.4030 |
0.5987 |
0.2328 |
-0.9344 |
-2.2816 |
-3.9170 |
-0.9578 |
-0.7414 |
0.6711 |
|
7h00m |
2.3894 |
0.6509 |
0.2531 |
-0.9291 |
-2.2816 |
-3.9171 |
-0.9577 |
-0.7580 |
0.6523 |
|
7h5m |
2.3746 |
0.7029 |
0.2733 |
-0.9234 |
-2.2816 |
-3.9171 |
-0.9575 |
-0.7745 |
0.6326 |
|
7h10m |
2.3587 |
0.7545 |
0.2934 |
-0.9172 |
-2.2816 |
-3.9172 |
-0.9573 |
-0.7909 |
0.6119 |
|
7h15m |
2.3417 |
0.8058 |
0.3133 |
-0.9106 |
-2.2816 |
-3.9172 |
-0.9571 |
-0.8071 |
0.5904 |
|
7h20m |
2.3236 |
0.8567 |
0.3331 |
-0.9035 |
-2.2816 |
-3.9173 |
-0.9569 |
-0.8231 |
0.5679 |
|
7h25m |
2.3043 |
0.9072 |
0.3528 |
-0.8961 |
-2.2816 |
-3.9173 |
-0.9567 |
-0.8388 |
0.5444 |
|
7h30m |
2.2840 |
0.9572 |
0.3722 |
-0.8882 |
-2.2816 |
-3.9173 |
-0.9565 |
-0.8541 |
0.5201 |
|
7h35m |
2.2626 |
1.0068 |
0.3915 |
-0.8799 |
-2.2815 |
-3.9174 |
-0.9563 |
-0.8690 |
0.4948 |
|
7h40m |
2.2401 |
1.0559 |
0.4106 |
-0.8711 |
-2.2815 |
-3.9174 |
-0.9561 |
-0.8834 |
0.4687 |
|
7h45m |
2.2165 |
1.1045 |
0.4295 |
-0.8620 |
-2.2815 |
-3.9175 |
-0.9559 |
-0.8971 |
0.4417 |
|
7h50m |
2.1919 |
1.1526 |
0.4482 |
-0.8524 |
-2.2815 |
-3.9175 |
-0.9557 |
-0.9103 |
0.4140 |
|
7h55m |
2.1662 |
1.2001 |
0.4667 |
-0.8424 |
-2.2815 |
-3.9176 |
-0.9555 |
-0.9227 |
0.3856 |
|
8h00m |
2.1395 |
1.2471 |
0.4850 |
-0.8321 |
-2.2815 |
-3.9176 |
-0.9553 |
-0.9343 |
0.3565 |
|
8h5m |
2.1118 |
1.2935 |
0.5030 |
-0.8213 |
-2.2815 |
-3.9176 |
-0.9551 |
-0.9451 |
0.3268 |
|
8h10m |
2.0831 |
1.3392 |
0.5208 |
-0.8101 |
-2.2815 |
-3.9177 |
-0.9549 |
-0.9550 |
0.2966 |
|
8h15m |
2.0534 |
1.3843 |
0.5384 |
-0.7986 |
-2.2815 |
-3.9177 |
-0.9548 |
-0.9640 |
0.2660 |
|
8h20m |
2.0227 |
1.4288 |
0.5557 |
-0.7867 |
-2.2815 |
-3.9178 |
-0.9546 |
-0.9720 |
0.2350 |
|
8h25m |
1.9911 |
1.4726 |
0.5727 |
-0.7744 |
-2.2815 |
-3.9178 |
-0.9544 |
-0.9790 |
0.2038 |
|
8h30m |
1.9585 |
1.5157 |
0.5895 |
-0.7617 |
-2.2815 |
-3.9179 |
-0.9542 |
-0.9850 |
0.1725 |
|
8h35m |
1.9250 |
1.5580 |
0.6060 |
-0.7487 |
-2.2815 |
-3.9179 |
-0.9540 |
-0.9900 |
0.1411 |
|
8h40m |
1.8905 |
1.5996 |
0.6222 |
-0.7353 |
-2.2815 |
-3.9179 |
-0.9538 |
-0.9939 |
0.1098 |
|
8h45m |
1.8552 |
1.6405 |
0.6381 |
-0.7216 |
-2.2815 |
-3.9180 |
-0.9536 |
-0.9969 |
0.0787 |
|
T UTC |
j |
k |
l |
m |
n |
dX/dt |
dY/dt |
cosw |
sinw |
|
8h50m |
1.8190 |
1.6806 |
0.6537 |
-0.7075 |
-2.2815 |
-3.9180 |
-0.9534 |
-0.9989 |
0.0477 |
|
8h55m |
1.7819 |
1.7198 |
0.6689 |
-0.6931 |
-2.2815 |
-3.9181 |
-0.9532 |
-0.9999 |
0.0171 |
|
9h00m |
1.7439 |
1.7583 |
0.6839 |
-0.6783 |
-2.2815 |
-3.9181 |
-0.9530 |
-0.9999 |
-0.0131 |
|
9h5m |
1.7052 |
1.7959 |
0.6985 |
-0.6632 |
-2.2815 |
-3.9181 |
-0.9528 |
-0.9991 |
-0.0428 |
|
9h10m |
1.6656 |
1.8327 |
0.7129 |
-0.6479 |
-2.2814 |
-3.9182 |
-0.9526 |
-0.9974 |
-0.0720 |
|
9h15m |
1.6252 |
1.8686 |
0.7268 |
-0.6322 |
-2.2814 |
-3.9182 |
-0.9524 |
-0.9949 |
-0.1006 |
|
9h20m |
1.5841 |
1.9036 |
0.7404 |
-0.6162 |
-2.2814 |
-3.9183 |
-0.9522 |
-0.9917 |
-0.1286 |
|
9h25m |
1.5422 |
1.9377 |
0.7537 |
-0.5999 |
-2.2814 |
-3.9183 |
-0.9520 |
-0.9878 |
-0.1559 |
|
9h30m |
1.4995 |
1.9709 |
0.7666 |
-0.5833 |
-2.2814 |
-3.9183 |
-0.9519 |
-0.9832 |
-0.1824 |
|
9h35m |
1.4562 |
2.0031 |
0.7792 |
-0.5664 |
-2.2814 |
-3.9184 |
-0.9517 |
-0.9781 |
-0.2082 |
|
9h40m |
1.4122 |
2.0344 |
0.7914 |
-0.5493 |
-2.2814 |
-3.9184 |
-0.9515 |
-0.9724 |
-0.2332 |
|
9h45m |
1.3674 |
2.0647 |
0.8032 |
-0.5319 |
-2.2814 |
-3.9185 |
-0.9513 |
-0.9663 |
-0.2574 |
|
9h50m |
1.3221 |
2.0940 |
0.8146 |
-0.5143 |
-2.2814 |
-3.9185 |
-0.9511 |
-0.9597 |
-0.2809 |
|
9h55m |
1.2761 |
2.1224 |
0.8256 |
-0.4964 |
-2.2814 |
-3.9186 |
-0.9509 |
-0.9528 |
-0.3035 |
|
10h00m |
1.2295 |
2.1497 |
0.8363 |
-0.4783 |
-2.2814 |
-3.9186 |
-0.9507 |
-0.9456 |
-0.3253 |
|
10h05m |
1.1823 |
2.1760 |
0.8465 |
-0.4599 |
-2.2814 |
-3.9186 |
-0.9505 |
-0.9381 |
-0.3464 |
|
10h10m |
1.1346 |
2.2013 |
0.8563 |
-0.4414 |
-2.2814 |
-3.9187 |
-0.9503 |
-0.9304 |
-0.3666 |
|
10h15m |
1.0863 |
2.2255 |
0.8658 |
-0.4226 |
-2.2814 |
-3.9187 |
-0.9501 |
-0.9224 |
-0.3862 |
|
10h20m |
1.0375 |
2.2487 |
0.8748 |
-0.4036 |
-2.2814 |
-3.9188 |
-0.9499 |
-0.9144 |
-0.4049 |
|
10h25m |
0.9882 |
2.2707 |
0.8834 |
-0.3844 |
-2.2814 |
-3.9188 |
-0.9497 |
-0.9062 |
-0.4229 |
|
10h30m |
0.9384 |
2.2918 |
0.8916 |
-0.3651 |
-2.2813 |
-3.9188 |
-0.9495 |
-0.8979 |
-0.4402 |
|
10h35m |
0.8882 |
2.3117 |
0.8994 |
-0.3456 |
-2.2813 |
-3.9189 |
-0.9493 |
-0.8895 |
-0.4569 |
|
10h40m |
0.8376 |
2.3305 |
0.9067 |
-0.3259 |
-2.2813 |
-3.9189 |
-0.9491 |
-0.8812 |
-0.4728 |
|
10h45m |
0.7865 |
2.3482 |
0.9136 |
-0.3060 |
-2.2813 |
-3.9190 |
-0.9489 |
-0.8728 |
-0.4881 |
|
10h50m |
0.7351 |
2.3648 |
0.9201 |
-0.2860 |
-2.2813 |
-3.9190 |
-0.9488 |
-0.8644 |
-0.5028 |
|
10h55m |
0.6834 |
2.3803 |
0.9261 |
-0.2659 |
-2.2813 |
-3.9190 |
-0.9486 |
-0.8560 |
-0.5169 |
|
11h00m |
0.6313 |
2.3946 |
0.9317 |
-0.2456 |
-2.2813 |
-3.9191 |
-0.9484 |
-0.8477 |
-0.5305 |
|
11h05m |
0.5789 |
2.4078 |
0.9368 |
-0.2252 |
-2.2813 |
-3.9191 |
-0.9482 |
-0.8395 |
-0.5434 |
|
11h10m |
0.5263 |
2.4199 |
0.9415 |
-0.2048 |
-2.2813 |
-3.9192 |
-0.9480 |
-0.8313 |
-0.5559 |
|
11h15m |
0.4734 |
2.4308 |
0.9458 |
-0.1842 |
-2.2813 |
-3.9192 |
-0.9478 |
-0.8232 |
-0.5678 |
|
11h20m |
0.4202 |
2.4405 |
0.9496 |
-0.1635 |
-2.2813 |
-3.9192 |
-0.9476 |
-0.8152 |
-0.5792 |
|
11h25m |
0.3669 |
2.4491 |
0.9529 |
-0.1428 |
-2.2813 |
-3.9193 |
-0.9474 |
-0.8072 |
-0.5902 |
|
11h30m |
0.3134 |
2.4565 |
0.9558 |
-0.1219 |
-2.2813 |
-3.9193 |
-0.9472 |
-0.7994 |
-0.6008 |
|
11h35m |
0.2597 |
2.4628 |
0.9583 |
-0.1011 |
-2.2813 |
-3.9194 |
-0.9470 |
-0.7917 |
-0.6109 |
|
T UTC |
A |
B |
C |
dD/dt |
D ' |
X ' |
Y ' |
|
5h05m |
2.2768 |
-0.1279 |
0.9656 |
-3.1409 |
16.6791 |
15.1118 |
-7.0588 |
|
5h10m |
2.2682 |
-0.0645 |
0.9919 |
-3.1085 |
16.4202 |
14.7873 |
-7.1385 |
|
5h15m |
2.2571 |
-0.0011 |
1.0189 |
-3.0746 |
16.1641 |
14.4629 |
-7.2182 |
|
5h20m |
2.2436 |
0.0622 |
1.0465 |
-3.0389 |
15.9108 |
14.1384 |
-7.2979 |
|
5h25m |
2.2275 |
0.1254 |
1.0749 |
-3.0016 |
15.6606 |
13.8139 |
-7.3775 |
|
5h30m |
2.2088 |
0.1882 |
1.1039 |
-2.9624 |
15.4135 |
13.4895 |
-7.4572 |
|
5h35m |
2.1874 |
0.2507 |
1.1336 |
-2.9214 |
15.1697 |
13.1650 |
-7.5368 |
|
5h40m |
2.1634 |
0.3128 |
1.1640 |
-2.8783 |
14.9295 |
12.8405 |
-7.6164 |
|
5h45m |
2.1365 |
0.3742 |
1.1951 |
-2.8331 |
14.6928 |
12.5161 |
-7.6960 |
|
5h50m |
2.1067 |
0.4350 |
1.2269 |
-2.7857 |
14.4601 |
12.1916 |
-7.7755 |
|
5h55m |
2.0741 |
0.4950 |
1.2594 |
-2.7359 |
14.2313 |
11.8671 |
-7.8551 |
|
6h00m |
2.0385 |
0.5540 |
1.2925 |
-2.6837 |
14.0068 |
11.5426 |
-7.9346 |
|
6h05m |
1.9998 |
0.6119 |
1.3263 |
-2.6290 |
13.7867 |
11.2181 |
-8.0142 |
|
6h10m |
1.9581 |
0.6686 |
1.3607 |
-2.5716 |
13.5712 |
10.8936 |
-8.0937 |
|
6h15m |
1.9133 |
0.7239 |
1.3957 |
-2.5115 |
13.3607 |
10.5691 |
-8.1732 |
|
6h20m |
1.8653 |
0.7776 |
1.4313 |
-2.4484 |
13.1552 |
10.2446 |
-8.2527 |
|
6h25m |
1.8142 |
0.8297 |
1.4674 |
-2.3824 |
12.9550 |
9.9201 |
-8.3321 |
|
6h30m |
1.7598 |
0.8797 |
1.5040 |
-2.3133 |
12.7605 |
9.5956 |
-8.4116 |
|
6h35m |
1.7022 |
0.9277 |
1.5410 |
-2.2411 |
12.5718 |
9.2711 |
-8.4910 |
|
6h40m |
1.6414 |
0.9734 |
1.5783 |
-2.1655 |
12.3892 |
8.9466 |
-8.5704 |
|
6h45m |
1.5774 |
1.0166 |
1.6159 |
-2.0866 |
12.2131 |
8.6221 |
-8.6498 |
|
6h50m |
1.5103 |
1.0570 |
1.6537 |
-2.0043 |
12.0436 |
8.2975 |
-8.7292 |
|
6h55m |
1.4400 |
1.0945 |
1.6916 |
-1.9185 |
11.8811 |
7.9730 |
-8.8085 |
|
7h00m |
1.3667 |
1.1288 |
1.7294 |
-1.8291 |
11.7258 |
7.6485 |
-8.8879 |
|
7h05m |
1.2904 |
1.1598 |
1.7671 |
-1.7363 |
11.5781 |
7.3239 |
-8.9672 |
|
7h10m |
1.2113 |
1.1871 |
1.8045 |
-1.6399 |
11.4382 |
6.9994 |
-9.0466 |
|
7h15m |
1.1295 |
1.2107 |
1.8415 |
-1.5401 |
11.3064 |
6.6749 |
-9.1259 |
|
7h20m |
1.0452 |
1.2302 |
1.8780 |
-1.4368 |
11.1831 |
6.3503 |
-9.2051 |
|
7h25m |
0.9586 |
1.2455 |
1.9138 |
-1.3301 |
11.0684 |
6.0258 |
-9.2844 |
|
7h30m |
0.8699 |
1.2564 |
1.9488 |
-1.2203 |
10.9628 |
5.7012 |
-9.3637 |
|
7h35m |
0.7793 |
1.2628 |
1.9827 |
-1.1073 |
10.8663 |
5.3767 |
-9.4429 |
|
7h40m |
0.6872 |
1.2644 |
2.0154 |
-0.9914 |
10.7794 |
5.0521 |
-9.5221 |
|
7h45m |
0.5938 |
1.2612 |
2.0469 |
-0.8729 |
10.7021 |
4.7275 |
-9.6013 |
|
7h50m |
0.4995 |
1.2531 |
2.0768 |
-0.7520 |
10.6348 |
4.4030 |
-9.6805 |
|
7h55m |
0.4046 |
1.2400 |
2.1051 |
-0.6289 |
10.5776 |
4.0784 |
-9.7597 |
|
8h00m |
0.3095 |
1.2220 |
2.1316 |
-0.5039 |
10.5306 |
3.7538 |
-9.8388 |
|
8h05m |
0.2147 |
1.1989 |
2.1563 |
-0.3775 |
10.4941 |
3.4293 |
-9.9180 |
|
8h10m |
0.1204 |
1.1709 |
2.1789 |
-0.2499 |
10.4681 |
3.1047 |
-9.9971 |
|
8h15m |
0.0271 |
1.1380 |
2.1993 |
-0.1216 |
10.4527 |
2.7801 |
-10.0762 |
|
8h20m |
-0.0647 |
1.1004 |
2.2176 |
0.0071 |
10.4480 |
2.4555 |
-10.1553 |
|
8h25m |
-0.1548 |
1.0583 |
2.2336 |
0.1357 |
10.4539 |
2.1309 |
-10.2344 |
|
8h30m |
-0.2428 |
1.0118 |
2.2473 |
0.2640 |
10.4704 |
1.8063 |
-10.3135 |
|
8h35m |
-0.3282 |
0.9611 |
2.2586 |
0.3914 |
10.4976 |
1.4817 |
-10.3925 |
|
8h40m |
-0.4108 |
0.9065 |
2.2677 |
0.5177 |
10.5353 |
1.1571 |
-10.4715 |
|
8h45m |
-0.4901 |
0.8484 |
2.2744 |
0.6424 |
10.5833 |
0.8325 |
-10.5505 |
Les deux tableaux suivants donnent les valeurs des
paramètres A, B, C, dD/dt, D, X et Y
avec un pas de tabulation de 5 minutes de temps. Les trois premiers paramètres
sont sans dimension, dD/dt est en secondes de degré par minute de temps,
D, X et Y sont en minutes de degré.
T UTC |
A |
B |
C |
dD/dt |
D ' |
X ' |
Y ' |
|
8h50m |
-0.5661 |
0.7869 |
2.2789 |
0.7653 |
10.6417 |
0.5079 |
-10.6295 |
|
8h55m |
-0.6383 |
0.7224 |
2.2811 |
0.8860 |
10.7101 |
0.1833 |
-10.7085 |
|
9h00m |
-0.7067 |
0.6552 |
2.2813 |
1.0043 |
10.7884 |
-0.1413 |
-10.7875 |
|
9h05m |
-0.7709 |
0.5857 |
2.2794 |
1.1198 |
10.8764 |
-0.4659 |
-10.8664 |
|
9h10m |
-0.8310 |
0.5141 |
2.2755 |
1.2324 |
10.9739 |
-0.7905 |
-10.9454 |
|
9h15m |
-0.8867 |
0.4409 |
2.2699 |
1.3419 |
11.0806 |
-1.1152 |
-11.0243 |
|
9h20m |
-0.9380 |
0.3663 |
2.2625 |
1.4482 |
11.1962 |
-1.4398 |
-11.1032 |
|
9h25m |
-0.9849 |
0.2905 |
2.2535 |
1.5511 |
11.3204 |
-1.7644 |
-11.1821 |
|
9h30m |
-1.0273 |
0.2140 |
2.2432 |
1.6506 |
11.4531 |
-2.0891 |
-11.2610 |
|
9h35m |
-1.0653 |
0.1370 |
2.2314 |
1.7466 |
11.5938 |
-2.4137 |
-11.3398 |
|
9h40m |
-1.0989 |
0.0598 |
2.2185 |
1.8390 |
11.7424 |
-2.7383 |
-11.4186 |
|
9h45m |
-1.1281 |
-0.0175 |
2.2045 |
1.9279 |
11.8985 |
-3.0630 |
-11.4975 |
|
9h50m |
-1.1531 |
-0.0945 |
2.1896 |
2.0133 |
12.0618 |
-3.3876 |
-11.5763 |
|
9h55m |
-1.1740 |
-0.1711 |
2.1738 |
2.0953 |
12.2320 |
-3.7123 |
-11.6551 |
|
10h00m |
-1.1908 |
-0.2471 |
2.1573 |
2.1738 |
12.4089 |
-4.0370 |
-11.7338 |
|
10h05m |
-1.2036 |
-0.3222 |
2.1402 |
2.2490 |
12.5921 |
-4.3616 |
-11.8126 |
|
10h10m |
-1.2127 |
-0.3964 |
2.1225 |
2.3209 |
12.7814 |
-4.6863 |
-11.8913 |
|
10h15m |
-1.2181 |
-0.4696 |
2.1044 |
2.3896 |
12.9766 |
-5.0109 |
-11.9701 |
|
10h20m |
-1.2200 |
-0.5414 |
2.0860 |
2.4553 |
13.1773 |
-5.3356 |
-12.0488 |
|
10h25m |
-1.2184 |
-0.6120 |
2.0673 |
2.5180 |
13.3833 |
-5.6603 |
-12.1275 |
|
10h30m |
-1.2137 |
-0.6811 |
2.0484 |
2.5778 |
13.5945 |
-5.9850 |
-12.2061 |
|
10h35m |
-1.2058 |
-0.7488 |
2.0293 |
2.6349 |
13.8104 |
-6.3096 |
-12.2848 |
|
10h40m |
-1.1950 |
-0.8148 |
2.0102 |
2.6893 |
14.0310 |
-6.6343 |
-12.3634 |
|
10h45m |
-1.1813 |
-0.8792 |
1.9911 |
2.7412 |
14.2560 |
-6.9590 |
-12.4421 |
|
10h50m |
-1.1649 |
-0.9419 |
1.9719 |
2.7907 |
14.4852 |
-7.2837 |
-12.5207 |
|
10h55m |
-1.1460 |
-1.0028 |
1.9529 |
2.8379 |
14.7183 |
-7.6084 |
-12.5993 |
|
11h00m |
-1.1247 |
-1.0620 |
1.9339 |
2.8828 |
14.9553 |
-7.9331 |
-12.6779 |
|
11h05m |
-1.1010 |
-1.1194 |
1.9151 |
2.9257 |
15.1960 |
-8.2578 |
-12.7564 |
|
11h10m |
-1.0752 |
-1.1749 |
1.8964 |
2.9665 |
15.4401 |
-8.5825 |
-12.8350 |
|
11h15m |
-1.0473 |
-1.2286 |
1.8779 |
3.0055 |
15.6875 |
-8.9072 |
-12.9135 |
|
11h20m |
-1.0175 |
-1.2804 |
1.8596 |
3.0426 |
15.9380 |
-9.2319 |
-12.9920 |
|
11h25m |
-0.9858 |
-1.3303 |
1.8415 |
3.0780 |
16.1916 |
-9.5566 |
-13.0705 |
|
11h30m |
-0.9524 |
-1.3783 |
1.8237 |
3.1118 |
16.4480 |
-9.8813 |
-13.1490 |
|
11h35m |
-0.9174 |
-1.4244 |
1.8061 |
3.1440 |
16.7072 |
-10.2060 |
-13.2275 |
Les deux tableaux suivants donnent les paramètres de réduction pour les instants des contacts et du maximum du passage géocentrique.
|
T UTC |
j |
k |
l |
m |
n |
dX/dt "/min |
dY/dt "/min |
cosw |
sinw |
|
5h 13m 33.157s |
2.4279 |
-0.4882 |
-0.1898 |
-0.9438 |
-2.2817 |
-3.9162 |
-0.9618 |
-0.4431 |
0.8965 |
|
5h 32m 49.815s |
2.4603 |
-0.2825 |
-0.1098 |
-0.9565 |
-2.2817 |
-3.9163 |
-0.9610 |
-0.4911 |
0.8711 |
|
8h 19m 43.545s |
2.0244 |
1.4264 |
0.5547 |
-0.7873 |
-2.2815 |
-3.9178 |
-0.9546 |
-0.9716 |
0.2367 |
|
11h 6m 37.141s |
0.5619 |
2.4118 |
0.9384 |
-0.2186 |
-2.2813 |
-3.9191 |
-0.9481 |
-0.8368 |
-0.5475 |
|
11h 25m 53.846s |
0.3573 |
2.4505 |
0.9535 |
-0.1390 |
-2.2813 |
-3.9193 |
-0.9474 |
-0.8058 |
-0.5921 |
|
T UTC |
A |
B |
C |
dD/dt "/m |
D ' |
X ' |
Y ' |
|
5h 13m 33.157s |
2.2606 |
-0.0194 |
1.0110 |
-3.0846 |
16.2379 |
14.5568 |
-7.1951 |
|
5h 32m 49.815s |
2.1970 |
0.2237 |
1.1206 |
-2.9394 |
15.2751 |
13.3058 |
-7.5022 |
|
8h 19m 43.545s |
-0.0597 |
1.1026 |
2.2167 |
0.0000 |
10.4480 |
2.4733 |
-10.1510 |
|
11h 6m 37.141s |
-1.0929 |
-1.1376 |
1.9090 |
2.9391 |
15.2746 |
-8.3629 |
-12.7819 |
|
11h 25m 53.846s |
-0.9799 |
-1.3390 |
1.8383 |
3.0842 |
16.2374 |
-9.6149 |
-13.0846 |