Fiche pédagogique n°05c :
Formulaires de calcul de la parallaxe solaire
à partir de l’observation des
distances entre Vénus et le centre du Soleil
J.-E. Arlot, P. Rocher (IMCCE) mercredi 12 janvier 2005
I.Introduction
Dans cette fiche nous allons donner un formulaire simple permettant de calculer une approximation de la parallaxe solaire (et donc l’Unité Astronomique ou UA) à partir de l’observation de la distance entre Vénus et le centre du Soleil. Contrairement au cas des contacts pour lequel nous avons besoin de deux observations éloignées, nous n’utiliserons qu’une seule observation avec la méthode dite « linéaire » qui compare la valeur observée de cette distance à la valeur théorique calculée. La différence entre ces deux valeurs nous permettra de corriger la valeur de la parallaxe solaire théorique utilisée dans les calculs. C’est en fait une méthode itérative mais nous nous limiterons à la dernière itération. Le but –pédagogique- de ce calcul, est de montrer que la valeur de l’UA calculée dépend de la qualité de la mesure de distance et aussi du lieu d’observation. Il sera intéressant de faire plusieurs calculs à partir d’observations faites à différents instants depuis le même lieu ou depuis des lieux éloignés pour comparer les valeurs obtenues et les moyenner.
Coefficients pré-calculés
Pour obtenir ce formulaire, nous avons pré calculé des paramètres A, B, C et D qui ne dépendent pas de la position des observateurs mais qui rendent compte des mouvements de Vénus et de la Terre autour du Soleil ainsi que du mouvement de rotation de la Terre autour de son axe. Attention, ils dépendent du temps et ont été tabulés en conséquence. Le paramètre dD/dt représente la variation instantanée de la distance du centre de Vénus au centre du Soleil. On peut donc ainsi calculer la valeur théorique de la distance mesurée et réduire l’observation (en déterminant une nouvelle valeur de la parallaxe –ou de l’UA-) en tenant compte du fait que les observateurs et les centres de Vénus, de la Terre et du Soleil ne sont pas dans le même plan et en intégrant le rapport des distances au Soleil et à Vénus donné par la troisième loi de Kepler. On trouvera ces tables à la fin de cette fiche.
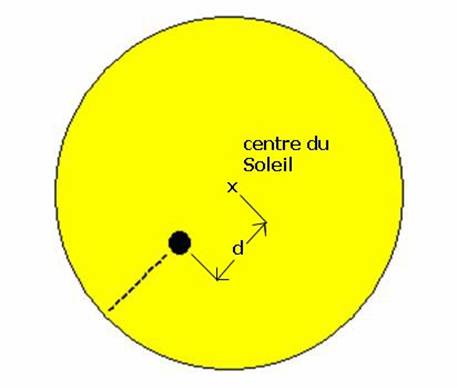
Valeur mesurée d entre Vénus et le centre du Soleil
II Observation de la distance de Vénus au centre du Soleil
Les données numériques dont vous devez disposer sont les suivants :
-
latitude et longitude du lieu d’observation (l, j)
-
la distance du centre de Vénus au centre du Soleil (voir figure ci-dessus)
en minutes de degré
-
l’instant de l’observation en Temps Universel (UTC)
Les formules à appliquer sont les suivantes :
- transformation de la latitude géographique j du lieu en latitude géocentrique j‘ :
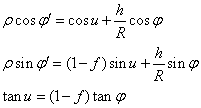
où h est l’altitude du lieu, R le rayon terrestre que l’on prendra égal à 6378,140 km et f l’aplatissement terrestre que l’on prendra égal à 1/298,257
et où cos u et sin u
sont déduits de tan u
- calcul de la valeur approchée Dp de la distance théorique Dc Vénus-Soleil
en utilisant les coefficients pré-calculés A, B, C et
D donnés en fin de fiche
![]() (F2)
(F2)
où p0 = 8,79414" et où r cos j’ et r sin j’ sont calculés ci-dessus
Attention, pour un calcul plus précis il faut introduire la valeur exacte de Dc : le calcul est beaucoup plus compliqué et vous pouvez faire appel à un serveur d’éphémérides (par exemple http://www.imcce.fr/page.php?nav=fr/ephemerides/formulaire/form_ephepos.php), calculer les positions du centre du Soleil et du centre de Vénus à l’instant de l’image analysée et en déduire la distance angulaire entre ces centres : c’est la distance Dc de la formule ci-dessus.
- calcul de la nouvelle parallaxe solaire et donc de la nouvelle UA :
Pour réduire cette observation nous allons utiliser la formule suivante:
![]() (F3)
(F3)
où D0 est notre mesure d exprimée en secondes de degré et A, B, C, dD/dt donné en fin de fiche
La parallaxe solaire déduite de notre observation est donc égale à p0 + dp0 soit 8,79414 + dp0
Pour faire le calcul, remplissez la feuille de calcul « distance » ci-après.
Feuille de calcul « distance » :
calcul de la parallaxe solaire à l’aide de l’observation
de la distance entre Vénus et le centre du Soleil
(moyenner un grand nombre d’observation est nécessaire pour obtenir un résultat correct)
longitude géographique l =
latitude géographique j =
distance observée (Vénus –
Soleil) : d = en
minutes de degré
instant de l’observation en
Temps Universel (UTC) =
- transformation de la
latitude géographique en latitude géocentrique :
(1) latitude géographique j =
(2) Calculez le cosinus de j :
cos (j
) =
(3) Calculez le sinus de j :
sin (j) =
(4) Altitude du lieu
d’observation h = en
mètres
(5) Calculez tan u = (1 –
1/298,257) x tan (ligne (1)) =
(6) Calculez l’angle u (qui
reste entre -90° et +90°) = arctan (ligne(5)) =
(7) Calculez le cosinus de u
= cos (ligne(6)) =
(8) Calculez le sinus de u =
sin (ligne(6)) =
(9) Calculez (r cos j’) = cos u +
(h/6378140) cos j
=
ligne (7) + [(ligne (4)/6378140) x ligne (2)] =
(10) Calculez (r sin j’) = (1 –
1/298,257) x sin u + (h/6378140) sin j
= (1 –
1/298,257) x ligne (8) + [(ligne(4)/6378140) x ligne (3)] =
- calcul de la distance
théorique « Vénus-Soleil » (ou bien
utilisez un serveur d’éphémérides et allez à la ligne 20) :
(11) Calculez le cosinus de l : cos l =
(12) Calculez le sinus de l : sin l =
(13) Calculez (r cos j’ cos l) = ligne (9) x ligne (11) =
(14) Calculez (r cos j’ sin l) = ligne (9) x ligne (12) =
(15) Déterminez A à partir de
la table en fin de fiche : A =
(16) Déterminez B à partir de
la table en fin de fiche : B =
(17) Déterminez C à partir de
la table en fin de fiche : C =
(18) Calculez le coefficient
de p0
dans la
formule (F2) :
=
ligne (15) x ligne (13) + ligne (16) x ligne (14) +ligne (17) x ligne (10) =
(19) Déterminez D à partir de
la table en fin de fiche : D =
(20) Calculez le deuxième membre
de la formule (F2) i.e. la valeur de Dthéorique :
= ligne (19) + 8,79414 x ligne
(18) =
- calcul de la nouvelle
parallaxe solaire :
(21) Votre mesure de dobservée en secondes de degré =
(22) La différence
« observé – calculé » = ligne (21) – ligne (20) =
(23) Correction de parallaxe
déduite de l’observation = ligne (22) / ligne (18) =
(24) Nouvelle parallaxe
solaire p0 = 8,79414 + ligne (25) =
- calcul de l’unité
astronomique :
(25) Calculez l’unité
astronomique :
UA
= ligne (24) x (206265,806247 / 6 378,1363) =
Vous pouvez refaire le calcul
pour d’autres valeurs observées et mesurées de la distance Vénus-Soleil
soit sur le même site, soit sur d’autres sites et moyenner les résultats
On rappelle que cette méthode n’est pas exacte, et que l’on doit utiliser des formules plus complexes pour réduire les observations (voyez les fiches n°4 et 5). Même si vos observations sont parfaites, vous n’obtiendrez qu’une valeur approchée de l’unité astronomique.
Coefficients pré-calculés à employer dans le formulaire ci-dessus :
Les deux tableaux suivants donnent les valeurs des
paramètres A, B, C, dD/dt,
D avec un pas de tabulation de 5 minutes de temps. Les trois premiers
paramètres sont sans dimension, dD/dt est en secondes
de degré par minute de temps, D est en minutes de degré.
|
T UTC |
A |
B |
C |
dD/dt |
D ' |
|
5h05m |
2.2768 |
-0.1279 |
0.9656 |
-3.1409 |
16.6791 |
|
5h10m |
2.2682 |
-0.0645 |
0.9919 |
-3.1085 |
16.4202 |
|
5h15m |
2.2571 |
-0.0011 |
1.0189 |
-3.0746 |
16.1641 |
|
5h20m |
2.2436 |
0.0622 |
1.0465 |
-3.0389 |
15.9108 |
|
5h25m |
2.2275 |
0.1254 |
1.0749 |
-3.0016 |
15.6606 |
|
5h30m |
2.2088 |
0.1882 |
1.1039 |
-2.9624 |
15.4135 |
|
5h35m |
2.1874 |
0.2507 |
1.1336 |
-2.9214 |
15.1697 |
|
5h40m |
2.1634 |
0.3128 |
1.1640 |
-2.8783 |
14.9295 |
|
5h45m |
2.1365 |
0.3742 |
1.1951 |
-2.8331 |
14.6928 |
|
5h50m |
2.1067 |
0.4350 |
1.2269 |
-2.7857 |
14.4601 |
|
5h55m |
2.0741 |
0.4950 |
1.2594 |
-2.7359 |
14.2313 |
|
6h00m |
2.0385 |
0.5540 |
1.2925 |
-2.6837 |
14.0068 |
|
6h05m |
1.9998 |
0.6119 |
1.3263 |
-2.6290 |
13.7867 |
|
6h10m |
1.9581 |
0.6686 |
1.3607 |
-2.5716 |
13.5712 |
|
6h15m |
1.9133 |
0.7239 |
1.3957 |
-2.5115 |
13.3607 |
|
6h20m |
1.8653 |
0.7776 |
1.4313 |
-2.4484 |
13.1552 |
|
6h25m |
1.8142 |
0.8297 |
1.4674 |
-2.3824 |
12.9550 |
|
6h30m |
1.7598 |
0.8797 |
1.5040 |
-2.3133 |
12.7605 |
|
6h35m |
1.7022 |
0.9277 |
1.5410 |
-2.2411 |
12.5718 |
|
6h40m |
1.6414 |
0.9734 |
1.5783 |
-2.1655 |
12.3892 |
|
6h45m |
1.5774 |
1.0166 |
1.6159 |
-2.0866 |
12.2131 |
|
6h50m |
1.5103 |
1.0570 |
1.6537 |
-2.0043 |
12.0436 |
|
6h55m |
1.4400 |
1.0945 |
1.6916 |
-1.9185 |
11.8811 |
|
7h00m |
1.3667 |
1.1288 |
1.7294 |
-1.8291 |
11.7258 |
|
7h05m |
1.2904 |
1.1598 |
1.7671 |
-1.7363 |
11.5781 |
|
7h10m |
1.2113 |
1.1871 |
1.8045 |
-1.6399 |
11.4382 |
|
7h15m |
1.1295 |
1.2107 |
1.8415 |
-1.5401 |
11.3064 |
|
7h20m |
1.0452 |
1.2302 |
1.8780 |
-1.4368 |
11.1831 |
|
7h25m |
0.9586 |
1.2455 |
1.9138 |
-1.3301 |
11.0684 |
|
7h30m |
0.8699 |
1.2564 |
1.9488 |
-1.2203 |
10.9628 |
|
7h35m |
0.7793 |
1.2628 |
1.9827 |
-1.1073 |
10.8663 |
|
7h40m |
0.6872 |
1.2644 |
2.0154 |
-0.9914 |
10.7794 |
|
7h45m |
0.5938 |
1.2612 |
2.0469 |
-0.8729 |
10.7021 |
|
7h50m |
0.4995 |
1.2531 |
2.0768 |
-0.7520 |
10.6348 |
|
7h55m |
0.4046 |
1.2400 |
2.1051 |
-0.6289 |
10.5776 |
|
8h00m |
0.3095 |
1.2220 |
2.1316 |
-0.5039 |
10.5306 |
|
8h05m |
0.2147 |
1.1989 |
2.1563 |
-0.3775 |
10.4941 |
|
8h10m |
0.1204 |
1.1709 |
2.1789 |
-0.2499 |
10.4681 |
|
8h15m |
0.0271 |
1.1380 |
2.1993 |
-0.1216 |
10.4527 |
|
8h20m |
-0.0647 |
1.1004 |
2.2176 |
0.0071 |
10.4480 |
|
8h25m |
-0.1548 |
1.0583 |
2.2336 |
0.1357 |
10.4539 |
|
8h30m |
-0.2428 |
1.0118 |
2.2473 |
0.2640 |
10.4704 |
|
8h35m |
-0.3282 |
0.9611 |
2.2586 |
0.3914 |
10.4976 |
|
8h40m |
-0.4108 |
0.9065 |
2.2677 |
0.5177 |
10.5353 |
|
8h45m |
-0.4901 |
0.8484 |
2.2744 |
0.6424 |
10.5833 |
T UTC |
A |
B |
C |
dD/dt |
D ' |
|
8h50m |
-0.5661 |
0.7869 |
2.2789 |
0.7653 |
10.6417 |
|
8h55m |
-0.6383 |
0.7224 |
2.2811 |
0.8860 |
10.7101 |
|
9h00m |
-0.7067 |
0.6552 |
2.2813 |
1.0043 |
10.7884 |
|
9h05m |
-0.7709 |
0.5857 |
2.2794 |
1.1198 |
10.8764 |
|
9h10m |
-0.8310 |
0.5141 |
2.2755 |
1.2324 |
10.9739 |
|
9h15m |
-0.8867 |
0.4409 |
2.2699 |
1.3419 |
11.0806 |
|
9h20m |
-0.9380 |
0.3663 |
2.2625 |
1.4482 |
11.1962 |
|
9h25m |
-0.9849 |
0.2905 |
2.2535 |
1.5511 |
11.3204 |
|
9h30m |
-1.0273 |
0.2140 |
2.2432 |
1.6506 |
11.4531 |
|
9h35m |
-1.0653 |
0.1370 |
2.2314 |
1.7466 |
11.5938 |
|
9h40m |
-1.0989 |
0.0598 |
2.2185 |
1.8390 |
11.7424 |
|
9h45m |
-1.1281 |
-0.0175 |
2.2045 |
1.9279 |
11.8985 |
|
9h50m |
-1.1531 |
-0.0945 |
2.1896 |
2.0133 |
12.0618 |
|
9h55m |
-1.1740 |
-0.1711 |
2.1738 |
2.0953 |
12.2320 |
|
10h00m |
-1.1908 |
-0.2471 |
2.1573 |
2.1738 |
12.4089 |
|
10h05m |
-1.2036 |
-0.3222 |
2.1402 |
2.2490 |
12.5921 |
|
10h10m |
-1.2127 |
-0.3964 |
2.1225 |
2.3209 |
12.7814 |
|
10h15m |
-1.2181 |
-0.4696 |
2.1044 |
2.3896 |
12.9766 |
|
10h20m |
-1.2200 |
-0.5414 |
2.0860 |
2.4553 |
13.1773 |
|
10h25m |
-1.2184 |
-0.6120 |
2.0673 |
2.5180 |
13.3833 |
|
10h30m |
-1.2137 |
-0.6811 |
2.0484 |
2.5778 |
13.5945 |
|
10h35m |
-1.2058 |
-0.7488 |
2.0293 |
2.6349 |
13.8104 |
|
10h40m |
-1.1950 |
-0.8148 |
2.0102 |
2.6893 |
14.0310 |
|
10h45m |
-1.1813 |
-0.8792 |
1.9911 |
2.7412 |
14.2560 |
|
10h50m |
-1.1649 |
-0.9419 |
1.9719 |
2.7907 |
14.4852 |
|
10h55m |
-1.1460 |
-1.0028 |
1.9529 |
2.8379 |
14.7183 |
|
11h00m |
-1.1247 |
-1.0620 |
1.9339 |
2.8828 |
14.9553 |
|
11h05m |
-1.1010 |
-1.1194 |
1.9151 |
2.9257 |
15.1960 |
|
11h10m |
-1.0752 |
-1.1749 |
1.8964 |
2.9665 |
15.4401 |
|
11h15m |
-1.0473 |
-1.2286 |
1.8779 |
3.0055 |
15.6875 |
|
11h20m |
-1.0175 |
-1.2804 |
1.8596 |
3.0426 |
15.9380 |
|
11h25m |
-0.9858 |
-1.3303 |
1.8415 |
3.0780 |
16.1916 |
|
11h30m |
-0.9524 |
-1.3783 |
1.8237 |
3.1118 |
16.4480 |
|
11h35m |
-0.9174 |
-1.4244 |
1.8061 |
3.1440 |
16.7072 |