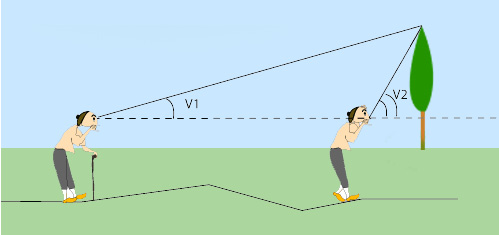

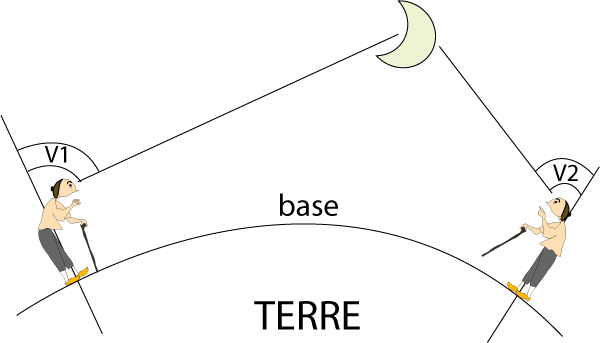
Calcul d'une distance par parallaxe
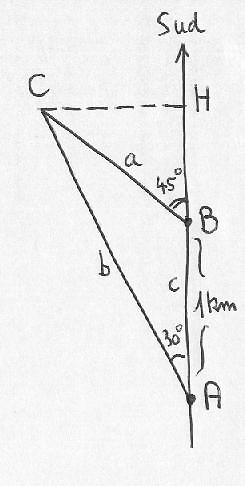
On désire mesurer la distance CH entre un bâtiment C et une route ABH de direction Nord-Sud sur laquelle se déplace un observateur qui ne peut mesurer que des angles ou des distances sur la route. D'une position A, l'observateur mesure un angle d'azimuth 30° entre la bâtiment C et la direction du Sud. D'une position B située un kilomètre plus loin sur la route, l'observateur va mesurer un azimuth de 45°. Pour calculer CH, il suffit de résoudre le triangle ABC pour calculer la distance CH connaissant les deux angles en A et B et la base AB. On applique une des relations entre angles et côtés dans un triangle.
a / sin(A) = b / sin(B) = c / sin(C) où (A), (B), (C) sont les
angles en A, B, C du triangle ABC.
On a donc:
a / sin(30°) = 1 km / sin(C) où (C) = 180° - ((A)+(B))
= 180° -165° = 15°
d'où: a = sin(30°) / sin(15°)
CH = a.cos(B) = cos(45°)
CH = 1366 m
On remarque alors que le mouvement diurne de rotation de la Terre autour
de son axe déplace chaque observateur au cours de la journée.
Ce déplacement va modifier l'angle sous lequel on voit un astre
à distance finie par rapport à l'angle de vue depuis le centre
de la Terre qui ne bouge pas. C'est la parallaxe diurne qui, pour un observateur
et un lieu donné va varier au cours de la journée. La distance
séparant deux positions d'un observateur peut servir de "base" pour
mesurer une distance. On comprend aisément qu'une telle base a une
valeur limite maximale: c'est le diamètre terrestre.
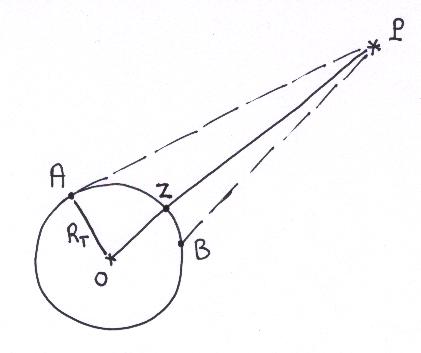
La parallaxe diurne a une valeur maximale: c'est la "parallaxe horizontale"
pour un astre donné. Elle sera atteinte pour un astre observé
à l'horizon. Cette valeur est donc l'angle sous lequel un observateur
situé sur l'astre en question voit le rayon terrestre.
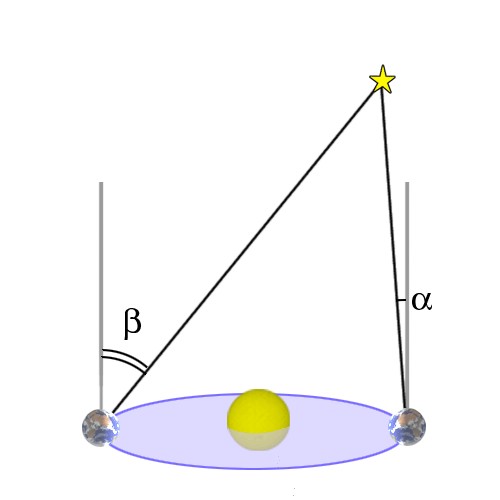
Mesure de la distance Terre-étoile grâce à la parallaxe annuelle due au mouvement de la Terre autour du Soleil
Cette mesure repose donc aussi sur la triangulation et la parallaxe
mais à 6 mois d'intervalle.
La mesure de parallaxe pour les étoiles est précise mais
elle n'est pas possible pour les étoiles très éloignées.
Ce sront alors des critères reposant sur les statistiques, la photométrie
et la spectroscopei qui permettront d'évaluer ces distances.
Parallaxe et distance Terre-Soleil
Ayant vu comment les astronomes mesurent les distances aux planètes et aux étoiles, comment va-t-on concrétement mesurer le système solaire tout entier? En quoi l'observation du passage de Vénus peut-elle nous donner la distance Terre-Vénus?
Pour comprendre, voyons concrètement comment on va mesurer la
parallaxe d'un astre donné.
On a vu qu'il fallait mesurer un angle de visée d'un astre par
rapport à une direction fixe, connue des deux observateurs, même
éloignés et sans contact. Cette direction fixe va être
fournie par un astre situé à proximité de l'astre
dont on veut mesurer la distance, mais situé suffisamment loin pour
pouvoir être considéré comme étant à
l'infini. Cela revient à dire que sa parallaxe est nulle: quel que
soit le lieu de la Terre d'où on l'observe, on le voit toujours
dans la même direction. On va donc utiliser les étoiles pour
laquelle la parallaxe diurne est négligeable. On a appliqué
cette méthode à la planète Mars dès le XVIIème
siècle mais la visée des étoiles était difficile
et on a cherché un autre astre et une méthode plus facile.
La planète Vénus, passant régulièrement devant
le Soleil, a apporté la solution. Lors d'un tel passage, le disque
solaire est un repère sur lequel la planète Vénus
va apparaître à des endroits différents pour des observateurs
différents. C'est le principe de la parallaxe.
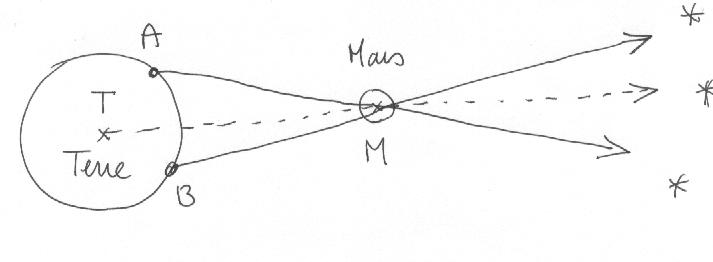
Cas de la planète Mars: celle-ci n'apparaît pas devant les mêmes étoiles selon le lieu d'observation sur Terre
Pour la planète Mars, seul le principe de la parallaxe avec un calcul utilisant une base connue (dépendant des lieux d'observation sur Terre) va nous permettre de calculer la distance Terre Mars.
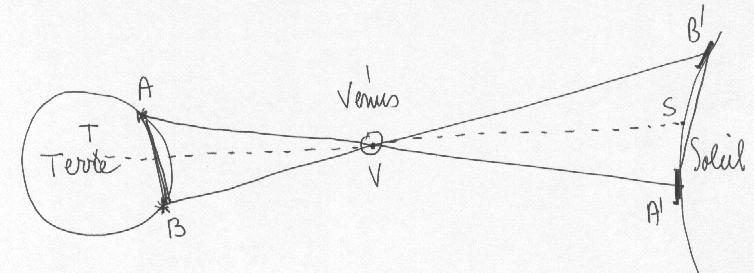
Cas de la planète Vénus: la projection de son disque sombre sur le disque solaire lors d'un passage n'est pas la même pour deux observateurs terrestres
Pour Vénus, on se sert du Soleil comme référence
pour calculer la parallaxe. A la différence du calcul de la parallaxe
pour la planète Mars, le Soleil n'est pas à l'infini: il
a lui aussi une parallaxe et il nous faut connaître le rapport des
distances du Soleil à Vénus et à la Terre. Cela nous
est fourni par les lois de Képler. On connait la distance AB, l'angle
en V (par l'observation) ainsi que le rapport VA/VA' (par la troisième
loi de Képler), on en déduit VT, VS et TS, d'où la
distance Terre-Soleil et l'unité astronomique. Le problème
se complique du fait que A et B bouge (rotation de la Terre autour de son
axe), ainsi que T et V (révolution de la Terre et de Vénus
autour du Soleil).
Les distances dans le système solaire et la troisième loi de Képler
Le principe de la parallaxe n'est pas suffisant à lui seul pour déterminer toutes les distances dans le système solaire: seules les planètes Mars et Vénus sont accessibles (et également les astéroïdes passant près de la Terre comme Eros). Le Soleil et les autres planètes sont trop éloignés pour cela. Ce sera grâce aux lois de Képler que le problème sera résolu.
La première loi de Képler énonce que les orbites des planètes autour du Soleil sont des ellipses. Nous l'utiliserons parce que les distances Terre-Vénus et Terre-Soleil vont donc varier au cours du temps selon la position de ces planètes sur leur orbite.
La deuxième loi de Képler est la loi des aires. Plus simplement, elle indique que les planètes vont plus vite sur leur orbite quand elles sont près du Soleil. Nous utiliserons cette loi pour l'analyse des observations de passage qui nécessite de connaître la vitesse angulaire apparente de vénus sur le disque solaire.
La troisième loi de Képler nous fournit les rapports entre
les distances au Soleil de toutes les planètes et il suffit ainsi
de connaître une seule distance dans le système solaire pour
connaître toutes les autres. Elle s'énonce ainsi:
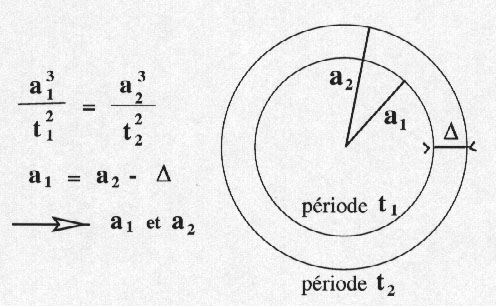
le rapport a3/T2 est constant pour toutes les
planètes du système solaire
où a est le demi grand axe de l'orbite et T la période
de révolution autour du Soleil. La figure ci-dessous montre ce qui
se passe si les orbites sont des cercles, connaissant la distance D
et les périodes t1 et t2.
La première loi de Képler énonce le fait que les
orbites sont des ellipses et on ne pourra donc pas assimiler les distances
Soleil-Terre et Soleil-Vénus aux demi-grands axes aT
et aV des orbites de la Terre et de Vénus. On passe du
demi grand axe "a" à la distance Soleil-planète (rayon vecteur)
"rP" par la formule:
rP = a (1 - e cos E) où e est l'excentricité
de l'ellipse et E caractérise l'emplacement de la planète
sur son orbite elliptique (variable appelée "anomalie excentrique").
D'autres considérations viennent compliquer le problème: du fait des perturbations gravitationnelles mutuelles, les planètes ne suivent pas les lois de Képler, valables uniquement pour deux corps, mais des plus complexes. De plus, ce n'est pas la Terre qui suit une trajectoire quasi-elliptique, mais le barycentre du système Terre-Lune. Enfin, la lumière ne se propage pas instantanément, ce qui nécessite la prise en compte de la distance Terre-Soleil, donc d'itérer le processus. La fiche n°32 fait le point sur la façon de mesurer et de définir l'unité astronomique aujourd'hui.
Conclusion
Le principe de la parallaxe et les lois de Képler (découvertes
par l'analyse des observations des positions des planètes au cours
du temps) sont donc suffisantes pour nous permettre de mesurer le distance
Terre-Vénus et, à partir de là, toutes les distances
des planètes au Soleil. La distance Terre-Soleil servant de base
pour le calcul de la distance aux étoiles proches, c'est l'univers
que nous pouvons donc envisager de mesurer désormais.