Fiche
pédagogique n°31b
Analyse des observations des contacts
Calcul de l’ua à partir de la base d’observations complètes :
P. Rocher, J.-E. Arlot, September 20, 2004.
Introduction.
Nous sommes maintenant après le 8 juin et disposons de toutes les observations de contact. Nous pouvons donc traiter un problème « non contraint », ou appliquer une méthode du type « Delisle » en utilisant que les « bonnes » observations. Pour cela nous devons trouver un critère qui nous permet de sélectionner les « bonnes » observations des temps de contact. Dans un premier nous ferons l’hypothèse que les « bonnes » observations sont celles qui sont proches des prédictions et nous vérifierons que cette hypothèse est fondée.
Puis à partir de plusieurs séries de bonnes observations extraites de la base générale, nous calculerons les valeurs de l’unité astronomique par la méthode non contrainte. Ensuite, pour tenir compte que toutes les observations n’ont pas le même impact sur le résultat, nous donnerons un poids à chacune de ces observations, ce qui nous permettra de calculer une moyenne pondérée de l’unité astronomique plus réaliste. Enfin, nous testerons la méthode de Delisle sur notre série de bonnes observations pour voir si elle s’applique bien dans le cas présent.
Le calcul de l’ua avec notre base de données des contacts
Les valeurs moyennes de l’ua que nous pouvons calculer, vont nous dire d’abord à quel point la valeur de la parallaxe que nous avons introduite dans le calcul théorique est bonne au regard de l’expérience que nous avons faite.
Comment procéder ?
Si la valeur que nous avons introduite est la bonne valeur, la moyenne de l’unité astronomique que nous calculons doit converger vers elle au fur et à mesure que l’on diminue la taille de l’intervalle de l’échantillon des écarts de temps de contacts autour des valeurs prédites.
Expliquons-nous : on extrait de toutes les données d’observations, les observations dont l’écart de temps avec les valeurs prédites sont, par exemple, inférieures à 30s de temps et l’on fait la moyenne des ua calculées avec ces observations. Puis on diminue de proche en proche la valeur de cet intervalle, on peut prendre ensuite par exemple 15, 8 secondes, puis 4 secondes et l’on fait à chaque fois la moyenne des ua calculées. Si la valeur de l’ua que nous avons introduite dans nos calculs est bonne, la suite des moyennes des ua que nous calculons doit converger vers notre valeur initiale. Parallèlement cela va se traduire sur les instants de contacts par un nombre de contacts en retard qui va approcher le nombre de contacts en avance et la moyenne de ces écarts va tendre vers zéro dans la mesure où la répartition des erreurs est gaussienne. L’analyse des données reçues va le montrer.
Voici les résultats que l’on obtient avec la base des observations telle qu’elle est au 14 juillet 2004.
Caractéristique de la base :
Nombre d'inscrits ayant envoyés leurs résultats : 1501.
Nombre d'inscrits ayant vu le premier contact : 722.
Nombre d'inscrits ayant vu le second contact : 1139.
Nombre d'inscrits ayant vu le troisième contact :1336.
Nombre d'inscrits ayant vu le quatrième contact :1170.
Nombre d'inscrits ayant mesuré la durée totale : 639.
Nombre d'inscrits ayant mesuré la durée interne: 1014.
Nombre d'inscrits ayant mesuré les quatre contacts: 616.
Nombre total d'observations : 4367.
Dans le tableau ci-dessous nous donnons successivement : la largeur de l’intervalle 2DT autour des valeurs des contacts prédites, le nombre d’observations répondant à ce critère, la moyenne de l’unité astronomique calculée, en résolvant le système non contraint, à l’aide de ces observations et la valeur de la parallaxe correspondante.
|
Largeur de l’intervalle |
Nombre
d’observations |
Moyenne des ua |
Écart à l’ua vraie |
Valeur de la
parallaxe |
|
60s |
2459 |
148511434 km |
1086436 km |
8,858482" |
|
30s |
1719 |
148789697 km |
808172 km |
8,841915" |
|
16s |
1066 |
149421803 km |
176067 km |
8,804510" |
|
8s |
583 |
149608708 km |
-10838 km |
8,793511" |
Tableau 1
Cette analyse des observations prouve que l’expérience confirme que la valeur initiale de la parallaxe utilisée (entrée dans les prédictions) est correcte et surtout cela confirme la qualité des prédictions faites avec cette valeur. Ce bon résultat résulte de deux choses : on a des observations très proches de la prédiction (8s) et on en a un grand nombre (1066).
Désormais la définition d’une bonne observation a changé : comme les bonnes observations sont celles qui sont proches de la réalité et que nos prédictions sont également proches de la réalité, les bonnes observations sont celles qui sont proches de nos prédictions. On a donc un critère de sélection objectif pour extraire les bonnes observations de notre base.
Ce résultat est issu de l’analyse des moyennes de 1501 observateurs représentant 4367 contacts. Il ne pouvait pas être obtenu directement en ligne au fur et à mesure que les observateurs entrent leurs valeurs car on ne connaissait pas par avance la précision des observations et le nombre de bonnes observations pour un intervalle donné. On ne savait pas non plus, si la répartition des erreurs allait suivre une loi normale, c’est-à-dire être gaussienne.
Résultats pour l’intervalle de 16s pour chaque contact :
Les tableaux suivants donnent successivement pour chaque contact puis pour tous les contacts le nombre d’observations correspondant à l’intervalle de 16s, le nombre d’observations en avance sur la prédiction et le nombre d’observations en retard sur la prédiction, puis la valeur moyenne de l’ua calculée avec ces observations, son écart-type et la parallaxe correspondant à la valeur de l’ua calculée.
|
Contact |
Nombre observations |
Nombre
d’observations en avance sur Tc |
Nombre
d’observations en retard sur Tc |
Moyenne des ua en km |
Écart à l’ua vraie en km |
Écart type sur la
moyenne des ua en km |
Parallaxe |
|
T1 |
104 |
49 |
55 |
149443844 |
154026 |
186773 |
8.803212" |
|
T2 |
262 |
128 |
134 |
149590268 |
7602 |
108359 |
8.794595" |
|
T3 |
421 |
187 |
234 |
149226725 |
371145 |
324822 |
8.816020" |
|
T4 |
279 |
130 |
149 |
149549752 |
48118 |
70599 |
8.796978" |
|
Tous |
1066 |
|
|
149421803 |
176067 |
252081 |
8.804510" |
Tableau 2.
On a donc, en utilisant tous les contacts de l’intervalle 16 sec, le résultat suivant : ua = 149421803 km +/- 252081 km
Pour calculer ces valeurs, on a fait la moyenne ![]() des valeurs
des valeurs ![]() de l’unité
astronomique calculées avec chaque observation.
de l’unité
astronomique calculées avec chaque observation.
![]()
Puis on a calculé la variance expérimentale ![]() et l’écart-type
et l’écart-type ![]() expérimental sur ces mesures de l’unité astronomique.
expérimental sur ces mesures de l’unité astronomique.
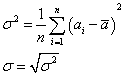
Enfin si l’on suppose que ![]() est une variable aléatoire qui suit une loi normale, c’est à
dire que les observations sont sans biais et que les erreurs sont des erreurs
normales indépendantes d’espérance mathématique nulle, alors
est une variable aléatoire qui suit une loi normale, c’est à
dire que les observations sont sans biais et que les erreurs sont des erreurs
normales indépendantes d’espérance mathématique nulle, alors ![]() est un bon estimateur
de l’unité astronomique et l’écart type
est un bon estimateur
de l’unité astronomique et l’écart type ![]() sur cet estimateur est donné par :
sur cet estimateur est donné par :
![]()
Attention il ne faut pas confondre l’écart type expérimental
s sur les mesures qui est indépendant
de la loi de distribution des observations et l’écart type ![]() sur l’estimateur qui
lui dépend de la loi de distribution observée.
sur l’estimateur qui
lui dépend de la loi de distribution observée.
On remarque que l’on a, comme prévu, une assez bonne répartition des observations avant et après les valeurs prédites. On remarque également la valeur de l’ua calculée à l’aide des observations du troisième contact est la plus mauvaise et que son écart type est supérieur à l’écart que l’on trouve entre la valeur vraie de l’ua et cette valeur calculée.
Le tableau 3 est identique au tableau 2 précédent, mais concerne les observations correspondant à l’intervalle de 8s.
|
Contact2Dt = 8s |
Nombre
d’obser-vations |
Nombre
d’observations en avance sur Tc |
Nombre
d’observations en retard sur Tc |
Moyenne des ua en km |
Écart à l’ua vraie |
Écart type sur la
moyenne des ua en km |
Parallaxe |
|
T1 |
60 |
23 |
37 |
149725155 |
-127285 |
131387 |
8.786672" |
|
T2 |
148 |
67 |
81 |
149618152 |
-20282 |
69271 |
8.792956" |
|
T3 |
225 |
102 |
123 |
149267460 |
330410 |
217813 |
8.813614" |
|
T4 |
150 |
76 |
74 |
150064685 |
-466815 |
55667 |
8.766792" |
|
Tous |
583 |
|
|
149608708 |
-10838 |
11835 |
8.793511" |
Tableau 3
On a donc sur tous les contacts de l’intervalle 8 sec, le résultat suivant : ua = 149608708 km +/- 11835 km
On remarque que pour chacun des contacts pris séparément les résultats ont tendance à se dégrader ; les valeurs de l’ua obtenues avec les contacts T3 et T4 présentent des écarts types inférieurs aux écarts que l’on a à la valeur exacte de l’ua. Par contre le résultat général issu de tous les contacts est meilleur.
Pourquoi a-t-on de forts écarts avec les résultats issus du troisième contact ?
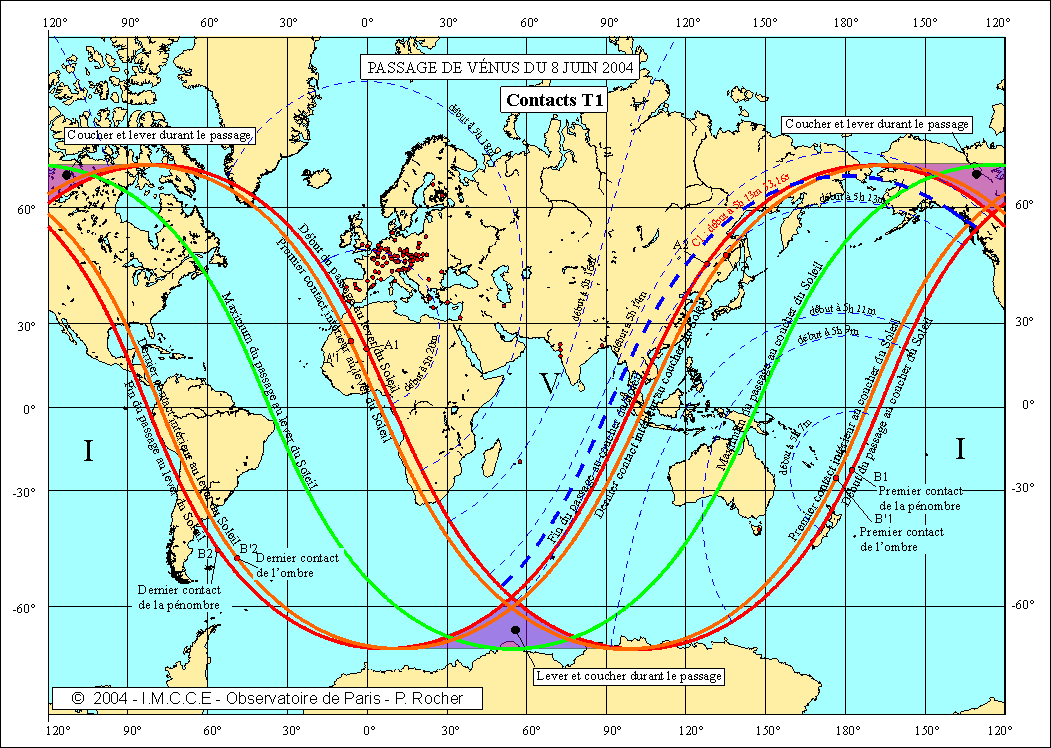
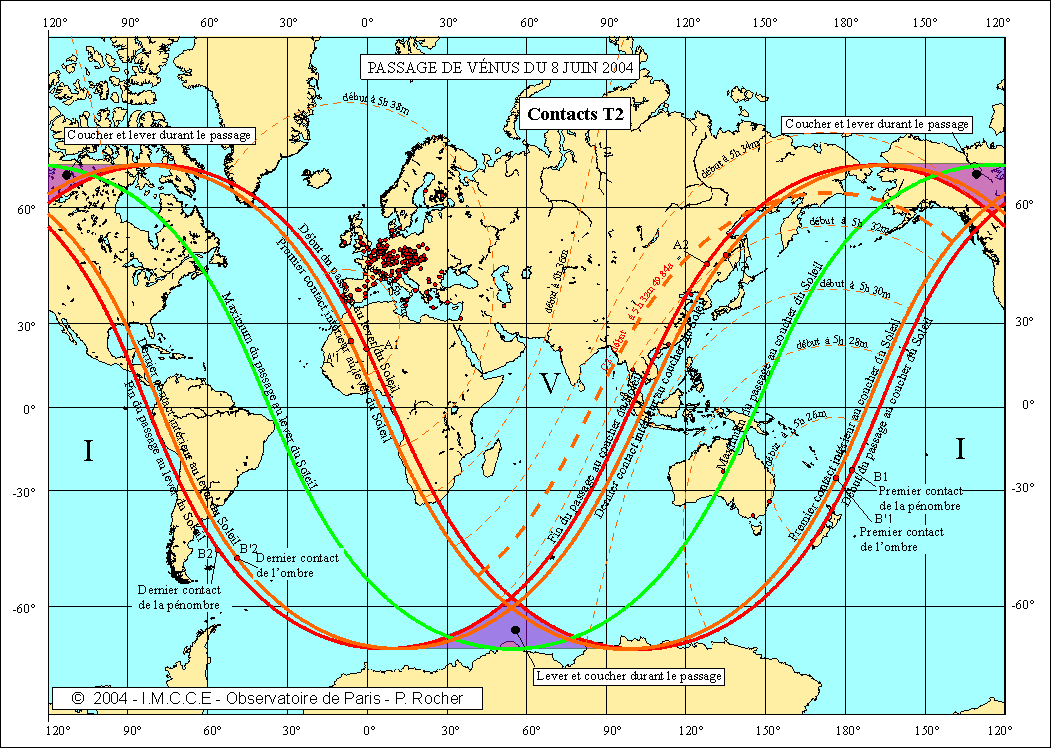
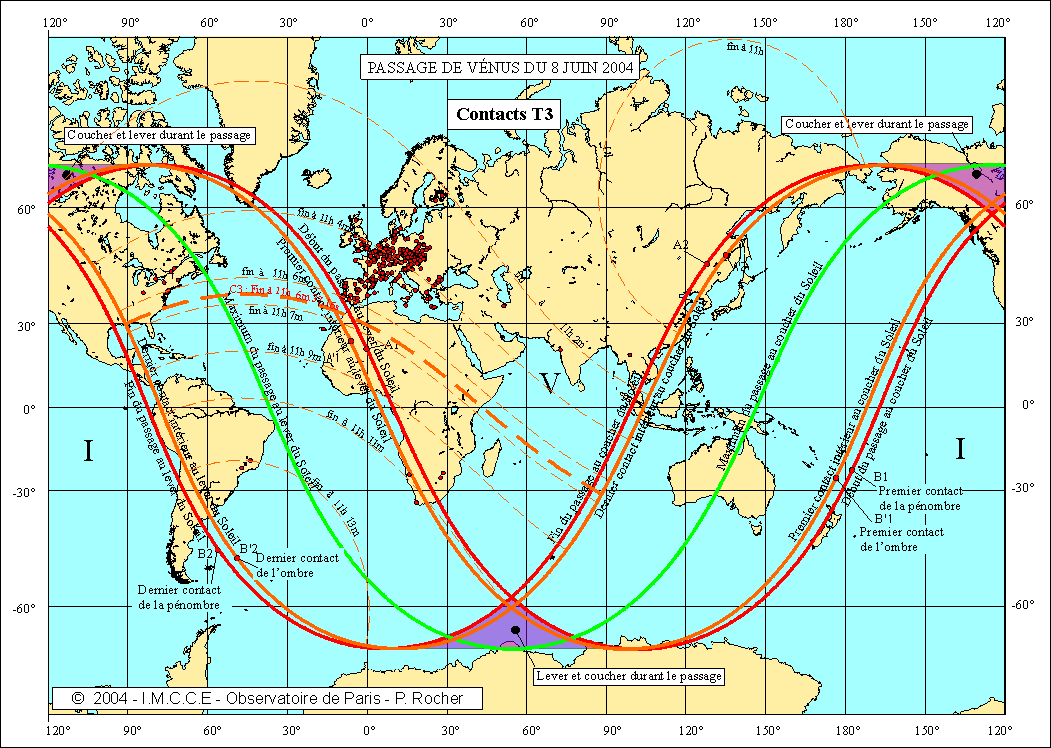
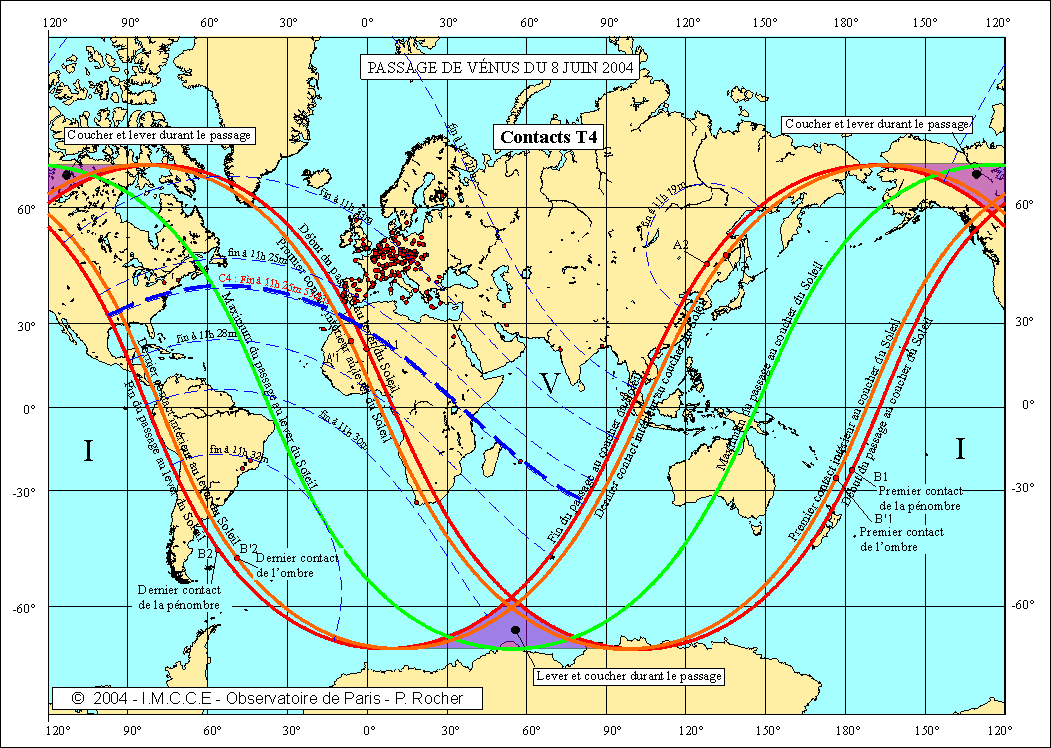
Tout simplement parce que de très nombreux lieux d’observations ont une parallaxe diurne faible au moment du troisième contact (Soleil haut sur l’horizon) et qu’ils sont relativement proches de l’intersection du cône d’ombre à l’instant du troisième contact géocentrique avec l’ellipsoïde terrestre. On peut visualiser cela sur une carte en traçant sur le globe les quatre courbes intersections des cônes d’ombre et de pénombre avec l’ellipsoïde terrestre aux instants des contacts géocentriques.
Plus un groupe d’observateurs est proche d’une de ces courbes, plus les effets de la parallaxe diurne pour le contact correspondant seront petits et plus la dispersion des mesures risque d’être grande si elle n’est pas compensée par de très bonnes mesures des contacts. De plus l’observation des instants des contacts intérieurs T3 est un peu plus difficile que celle des contacts extérieurs T4 du fait de la goutte noire. Ainsi les contacts T3 et T4 devraient être plus faciles à observer que les contacts T1 et T2 puisque la majorité des observateurs les ont observé haut dans le ciel, mais, bien que meilleures (225 observations retenues ici pour T3 contre 148 pour T2) ces observations donnent de plus mauvais résultats, justement parce que le Soleil est proche du zénith.
Moyenne pondérée.
Dans le calcul précédent, nous nous sommes contentés de faire la moyenne de toutes les valeurs de l’unité astronomique calculées et nous avons attribué le même poids à chaque résultat. Or on sait que les erreurs d’observations faites, pour un contact donné, depuis un lieu mal situé peuvent générer des écarts importants dans les résultats. Ainsi une erreur aléatoire de quelques secondes sur la mesure d’un contact peut avoir des effets plus ou moins forts sur la valeur de l’ua calculée.
Nous allons donc essayer de pondérer ces résultats en donnant un poids à chaque observation, ce poids sera d’autant plus faible que le lieu est mal situé pour un contact considéré.
Si l’on suppose que les observations sont faites sans biais avec une erreur aléatoire de t. Alors les écarts types sur la parallaxe ou l’unité astronomique peuvent être estimés, pour chaque observation, par :
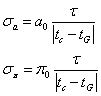
où tc est l’instant du contact topocentrique calculé et tG est l’instant du contact géocentrique.
On peut prendre comme poids de chaque observation : ![]()
Alors les moyennes pondérées de l’unité astronomique et de la parallaxe se calculent à partir des valeurs individuelles a(k) ou p(k) calculées pour chaque observation k à l’aide des deux relations suivantes :
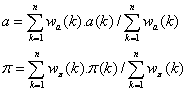
et les écarts types sur les moyennes pondérées sont données par :
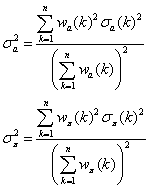
Voici les résultats obtenus sur l’échantillon des 1066 observations des
contacts comprises dans l’intervalle 16 secondes autour des valeurs prédites et
si l’on suppose que l’erreur aléatoire sur chaque observation est de +/- 5s. Ce
tableau est à comparer avec le tableau 2.
|
Contact |
Nombre observations |
ua moyenne pondérée
en km |
Écart à l’ua vraie en km |
Écart type sur la
moyenne de l’ua en km |
Parallaxe |
Écart type sur la
moyenne de la parallaxe |
|
T1 |
104 |
149491052 |
106818 |
194889 |
8,800432" |
0,011457" |
|
T2 |
262 |
149564790 |
33080 |
114908 |
8,796093" |
0,006755" |
|
T3 |
421 |
149424892 |
172978 |
231528 |
8,804328" |
0,013610" |
|
T4 |
279 |
149312924 |
284946 |
285616 |
8,810931" |
0,016790" |
|
Tous |
1066 |
149507347 |
90523 |
86718 |
8,799473" |
0,005098" |
Tableau 4
Si l’on fait l’hypothèse que l’erreur aléatoire sur chaque observation est de +/- 10s, alors on obtient les résultats suivants :
|
Contact |
Nombre observations |
ua moyenne pondérée
en km |
Écart à l’ua vraie en km |
Écart type sur la
moyenne de l’ua en km |
Parallaxe |
Écart type sur la
moyenne de la parallaxe |
|
T1 |
104 |
149491052 |
106818 |
389778 |
8,800432" |
0.022913" |
|
T2 |
262 |
149564790 |
33080 |
229816 |
8,796093" |
0.013510" |
|
T3 |
421 |
149424892 |
172978 |
463056 |
8,804328" |
0.027221" |
|
T4 |
276 |
149312924 |
284946 |
571233 |
8,810931" |
0.033580" |
|
Tous |
1066 |
149507347 |
90523 |
173437 |
8,799473" |
0.010196" |
Tableau 4 bis
On constate que les moyennes pondérées ne changent pas mais que les écarts types sur ces moyennes ont doublé, d’où l’importance de l’estimation de l’erreur de mesure dans les observations des temps de contact.
Globalement la moyenne pondérée donne de meilleurs résultats puisque les mauvais lieux d’observation ont moins de poids. Ce n’est pas vrai pour les contacts pris individuellement.
Utilisation de la méthode de Delisle sur la base d’observation.
Nous pouvons maintenant extraire de la base générale une base d’observations sélectionnées qui nous permettra d’appliquer la méthode de Delisle.
Considérons la base construite à l’aide des observations se trouvant dans l’intervalle 16s pour les contacts. On a donc 104 observations du premier contact, 262 observations du second contact, 421 observations du troisième contact et 276 équations du quatrième contact. Toutes ces observations sont indépendantes.
La méthode de Delisle consiste, pour chaque contact, à combiner deux à deux les observations dont l’écart de temps de contact est important. En faisant cela nous construisons pour chaque contact des séries d’observations qui ne sont plus indépendantes, une même observation pouvant être combinée avec de nombreuses autres.
Nous avons combiné entres elles toutes des observations qui présentaient un écart supérieur ou égal à 6 minutes de temps.
Cela à permis de construire 103 combinaisons d’observations pour le premier contact, 1531 combinaisons d’observations pour le second contact, 1979 combinaisons d’observations pour le troisième contact et 773 combinaisons d’observations pour le quatrième contact. Soit un total de 4386 combinaisons d’observations.
Comme l’on combine des observations, on doit pondérer les
résultats pour prendre en compte le fait qu’une même observation puisse être
utilisée plusieurs fois. Il convient donc de donner un poids à chaque
combinaison d’observations. De nouveau si l’on suppose que les observations
sont faites sans biais avec une erreur aléatoire de t. Alors l’erreur sur la différence de temps de contact est de ![]() et les écarts types sur chaque parallaxe et ua calculée sont
donnés par :
et les écarts types sur chaque parallaxe et ua calculée sont
donnés par :
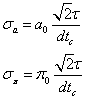
a0 et p0
étant l’unité astronomique et la parallaxe de référence et dtc
la différence des instants de contact calculés. Le choix d’une combinaison
statistique optimale n’est pas simple, un bon compromis consiste à prendre un
poids moyen entre les combinaisons en donnant un poids ![]() à la k ième
combinaison.
à la k ième
combinaison.
Alors les valeurs de l’ua et de la parallaxe se calculent à partir des valeurs individuelles a(k) ou p(k) calculées pour chaque combinaison k à l’aide des deux relations suivantes :
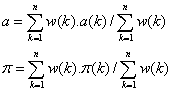
n étant le nombre de combinaisons pour un contact donné.
Les équations n’étant plus indépendantes on doit construire la matrice des coefficients de corrélations reliant les différentes combinaisons d’observations, cette matrice est d’ordre n pour chaque contact, n étant le nombre de combinaisons construites pour le contact considéré. Dans cette matrice, il est facile de comprendre que le coefficient de corrélation r(k,k’) entre le résultat k obtenu à partir de la combinaison (i,j) de deux observations et le résultat k’ obtenu à partir de la combinaison de deux observations (i’,j’) est nul si (i,j) sont différents de (i’j’) (aucune observation commune), est égal à 0,5 si (i,j) est combiné avec (i,j’) ou (i’,j) et est égal à –0,5 si (i,j) est combiné avec (j’,i) ou (j,i’). La matrice est donc symétrique et les écarts types sur les moyennes pondérées sont donnés par :
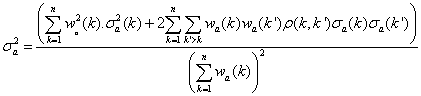
et
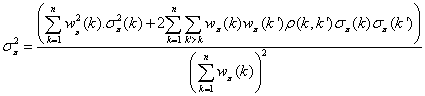
Le tableau suivant nous donne les résultats obtenus sur l’échantillon en supposant que l’erreur aléatoire sur l’observation de chaque contact est de +/-5s.
|
Contact |
Nombre de
combinai-sons |
Moyenne pondérée des
ua en km |
Écart à l’ua vraie en km |
Écart type de la
moyenne en km |
Parallaxe |
Écart type de la
parallaxe |
|
T1 |
103 |
149593369 |
4501 |
1308668 |
8.794413" |
0.076930" |
|
T2 |
1531 |
149604208 |
-6338 |
535661 |
8.793775" |
0.031489" |
|
T3 |
1979 |
150623168 |
-1025298 |
423861 |
8.734286" |
0.024917" |
|
T4 |
773 |
148904105 |
693765 |
534664 |
8.835121" |
0.031430" |
|
Tous |
4386 |
149840958 |
-243088 |
310577 |
8.779881" |
0.018257" |
Tableau 5
On a donc sur tous les contacts le résultat suivant : ua = 149840958 km +/- 310577 km, ce résultat est à comparer avec la valeur obtenue à l’aide des observations non combinées : ua = 149421803 km +/- 252081 km ou plutôt avec le résultat obtenu en faisant la moyenne pondérée : ua = 149507347 km +/- 86718 km.
On constate que dans le cas présent, c’est-à-dire en faisant la combinaison des observations dont la différence des contacts est supérieure à 6 minutes, la méthode de Delisle n’améliore pas les résultats. Les moyennes calculées à l’aide des contacts T1 et T2 deviennent très bonnes mais ont des écarts types très forts. Cela provient du fait que l’on ne combine que quelques observations présentant un fort écart de temps de contact (une seule dans le cas de T1 et six dans le cas de T2) avec toutes les observations européennes. Les écarts de temps de contacts sont très grands (supérieurs à 12 minutes), toutes les combinaisons ont sensiblement le même poids, par contre il y a une très forte corrélation dans ces combinaisons, cela se traduit par de très forts écarts types (surtout pour T1). On observe un phénomène du même ordre pour les contacts T3 et T4, de nouveau on a très peu d’observations présentant un fort écart avec les observations européennes (six pour T3 et trois pour T4), mais cette fois les écarts de temps de contacts sont plus faibles (de 6 à 9 minutes).
Les résultats auraient été différents si, comme aux siècles passés, l’on avait envoyé des observateurs en des lieux bien particuliers. En effet notre base d’observateurs présente deux gros défauts : premièrement une très forte dissymétrie avec de très nombreux observateurs européens et très peu d’observateurs présentant de grands écarts de temps de contact avec ce groupe important, deuxièmement on a très forte proportion d’observations du troisième contact et quatrième contact avec une parallaxe diurne faible (Soleil haut sur l’horizon) et avec des lieux proches des courbes C3 et C4.
Malgré cela les résultats sont assez satisfaisants car l’on retrouve la valeur de l’ua et de la parallaxe avec une précision qui correspond à celle escomptée en utilisant ces méthodes d’observations. C’est également la preuve que les observations ont été bien faites (à l’exception des tests de dernières heures et des valeurs aberrantes). Il ne semble pas y avoir eu de tricherie, personne n’a trouvé tous ses contacts avec une très bonne précision.
Les quatre cartes suivantes donnent pour chaque contact, les courbes correspondant à un contact à un instant t donné. On a tracé en plus gras les courbes C1, C2, C3 et C4 correspondant aux lieux sur la Terre observant les contacts au même instant que le centre de la Terre. Nous avons également tracé sur ces cartes les lieux d’observations retenus pour nos résultats et possédant un écart inférieur à 8 secondes avec les prédictions (intervalle 2DT = 16s).
Certes, la méthode de Delisle n’est pas très performante d’un point de vue statistique, mais elle garde tout son intérêt pédagogique. Nous avons donc extrait de la base générale comportant toutes les observations, une base formée par les « bonnes observations ». Sur cette base les élèves pourront utiliser la méthode de Delisle sur deux observations de leur choix et s’apercevoir ainsi que tous les sites d’observation ne sont pas équivalents, même à précisions de mesure égales.
En conclusion :
Pour conclure, que pouvons-nous dire des résultats obtenus ? Les meilleurs résultats sont les suivants :
UA = 149 608 708 km +/- 11 835 km (diff. à l’UA vraie
10 838 km)
pour le système non contraint linéarisé (583 observations dans un intervalle de 8s)
UA= 149 840 958 km +/- 310 577 km (diff. à l’UA vraie 243 088 km)
pour la méthode de Delisle avec tous les contacts (4386 combinaisons à partir de 1066 observations dans un intervalle de 16s).
Comme prévu, la méthode de calcul avec linéarisation et
traitement de chaque observation par comparaison à une valeur théorique donne
le meilleur résultat. Cela vient du fait que nous n’avons pas pu choisir les
sites d’observation mais que les observations ont cependant été réalisées avec
une très bonne précision. Par ailleurs, si on diminue l’intervalle de sélection
des observations (moins de 8s), le nombre de données est insuffisant et la
qualité du résultat est moindre.