Written on Venus's transit of 1761

Preparation of the transit observations of 1761

Observations of 1761

1761 observations analysis

Preparation of the transit observations of 1761

Gregory 1663, Scholium [[gregory-p130 ]]

The Scottish James Gregory (1638-1675) published a treatise of advanced optics (Optica promota) in 1663. By a simple remark (Scholium) at the end of proposition 87, he evokes the possibility to determine the solar parallax : "This problem might have some very nice applications but might be difficult to perform from transit observations of Venus or Mercury, when the planets shadow a very small fraction of the Sun. [during the transit]. This could indeed lead to the search for the Sun’s parallax."

Halley

The young Edmond Halley (1656-1743) is sent in 1677 at the Saint-Helen island for the observations of Mercury’s transit, where he is the first to observe a complete transit. Following the idea suggested by Gregory in 1663, he elaborated a method to determine the Sun’s parallax from the measurements of transit durations, observed from two places very far from each other.

He published in 1716 a “fundamental” text, which will become a reference text for all observers. This Latin text (Methodus singularis, qua Solis parallaxis sive distantia a Terra ope Veneris intra Solem conspiciendae tuto determinari poterit = "Singular method to precisely determine the Sun’s parallax or its distance to Earth by observations of Venus on the Sun"), only encompasses the results of his calculations. The precision should reach 1/500 (quingentesimam p. 455) so that, according to him, the time span between two internal contacts can be determined "at less than a 1 s precision" (etiam absque errore unius minuti secundi temporis, page 457). As he should be dead by 1761 (nobis vita functis, page 460), he called for the collaboration of all English, French, and Dutch astronomers (page 460). He assumed a value of the Sun’s parallax of 12,5" (duodecim secundorum cum semisse, page 456), and computed that the transit durations will be different by 17 minutes (septendecim minutis, page 459) between Port Nelson (90° West London) and the Gange’s delta (90° East).

Three versions of this important text are presented here : the original version from Halley, in Latin (1716), an English translation (1760), a French translation (2003).

Halley 1716, Ph.tr.-29, 1716, p. 454-464 [[ Ph.tr.-29, 1716, p. 455-464 ]] (page 454 is missing ; the corresponding text is reproduced below).

The beginning of the text, at the bottom of page 454, is the following :

Methodus singularis, quâ Solis Parallaxis sive distantia à Terra, ope Veneris intra Solem conspiciendae, tuto determinari poterit : proposita coram Regia Societate ab Edm. Halleio J. U. D. ejusdem Societatis Secretario.

Plurima sunt maxime quidem paradoxa, omnemque fidem apud vulgus superantia, quae tamen adhibitis. Mathematicarum Scientiarum principiis levi negotio enodantur. Ac sane nullum problema magis arduum ac difficile videbitur, quam est Solis à Terra distantiam vero proximam determinare ; quod tamen obtentis accuratis /

(455) quibusdam observationibus...[[ Ph.tr.-29p.455-464 ]] and Figure [[ Ph.tr.-29p.428-428b]]

Halley 1716 (Ferguson, in English) [[ 1605-(014 à 026) ]]

The text of Halley was translated from Latin to English and published in 1760 by James Ferguson (1710-1776) in his book "Astronomy" (see Article III, pages 316 to 327). Ferguson corrected the original schematic of Halley by drawing the apparent trajectory of Venus with a correct inclination with respect to the equator (14° 38' instead of 2° 18' for the Halley version) and by using some different notations. Please note a typographic mistake (page 325, line 20) : it should be read 14' 41" instead of 14' 4". Ferguson’s book which encompasses a lot of other information about Venus transits is presented further in this text.

[1605] Ferguson James, Astronomy explained upon Sir Isaac Newton’s principles, and made easy to those who have not studied mathematics. A plain method of finding the distances of all the planets from the sun, by the transit of Venus over the Sun’s disc, in the year 1761. 3rd edition, London, 1764. English text (502 pages).

Halley 1716 (in French) [[ Halleytrad ]] No French translation of the text from Halley was published so far. This comes from the fact that the French astronomers that prepared the 1761 transit observations knew perfectly well Latin ; hence they did not need any complete French translation. Then, the methods used to compute parallaxes evolved since 1716 and were different than the one used by Halley. A complete Latin to French translation of the text is presented here. The schematic that comes along [[ fichier-schema-Halley-fr.bmp ]] is a French translation of the schematic of the original article from Halley.

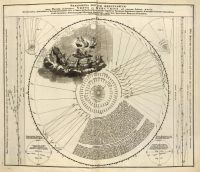
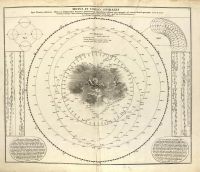
Doppelmayer 1742, Atlas [[  00047-(003à005) ]]

The German Johann Gabriel Doppelmayer (1671-1750), published in Nüremberg in 1742 a compilation of several astronomical diagrams : Atlas novus coelestis. On plate 7 (Phaenomena motuum irregularium) [[ 003  ]], he drew the heliocentric orbits of Mercury, Venus and the Earth, with the retrograde motion loops for the year 1710 (inner conjunction with the Sun). He presents the schematics of the Venus transit expected for 1761 (fig. iii), and the one of the Mercury transit of November 1710 (fig. iv), which was actually not visible in Europe. Plate 9 (Motus in coelo spirales) [[004  ]] represents the geocentric orbits of the Sun, Mercury and Venus, clearly showing their distance variations to the Earth. Doppelmayer drew several retrograde motion loops for Mercury in 1712 (February 5, June 6 and October 6, 1712) and for Venus (June 20, 1713 and January 27, 1715). These two last loops are the closer to the Earth, and are presented in the middle of the figure. On the allegoric drawing, Mercury (right) and Venus (left) are on seesaws, pushed by the Sun… Fig. 9 on Plate 13 [[ 005 ] ]] is not a good reproduction of the Horrocks drawing of the Venus transit of 1639 : the position of the planet on the Sun's disc is wrong.

[00047] Doppelmayer J. G., Atlas novus coelestis, Nüremberg, 1742, in Latin.

Delisle, world map, Mercury 1753

Joseph-Nicolas Delisle (1688-1768) drew a map of the world indicating the visibility zones of the Venus transit of May 6, 1753 in Asia, and then in Europe and Africa.

Delisle, manuscripts 1753 and 1760 [[ A-3-12-34b-(001à039) ]]

Manuscript of the memorandum read at the Science Academy in 1760 : "La Description et l'usage de la mappemonde dressée pour le passage de Vénus sur le disque du Soleil qui est attendu le 6 juin 1761". (Description and use of the world map established for the transit of Venus on the Sun’s disc, expected on June 6, 1761)

Another manuscript [[ A-3-12-34b-(037) ]], from May 6, 1753 : "Avis très importants aux astronomes sur le passage de Vénus au devant du Soleil qu'ils attendent le 6 juin 1761" (Very important warning to astronomers about the transit of Venus in front of the Sun, expected on June 6, 1761).

 

[A-3-12-34b] Delisle, Manuscripts 1753 and 1761 : Mémoires sur le passage de Vénus de 1761 (Memorandum on the Venus transit of 1761).

Anonymous, HMARS 1757 p. 77-99 (History part) [[HMARS-1757 p.76-99 ]]

These pages describe the history of previous Mercury and Venus transits and the preparation of the missions of 1761, in particular the choice of Tobolsk and Rodriguez Island observing sites (pages 89 to 93).

Computations from Lalande predicted a time span of 17 minutes between the instants of the first internal contact observed at the Mecca and at the Easter Island, which are two sites nearly located at the antipodes (p. 88). In reality, the transit occurred during the night at the Easter Island.

Lalande 1757, HMARS 1757 p. 232-253 [[ HMARS-1757 p.232-253 ]]

Joseph-Jérôme de Lalande (1732-1807) got deeply involved in the prediction of transits of 1761 and 1769. In 1757, he published a Mémoire sur les passages de Vénus (Memorandum on Venus transits), in which he explains a graphical method to determine the parallax effect during Venus’ transit. He assumes a value of the solar parallax of 10" (page 234). Next, he draws a map (page 239) and indicates the values of the parallax with the help of different arcs that permit a direct reading without calculations.

For the 1769 transit, Lalande (page 244) predicted that the largest parallax differences should occur at (Saint) Petersburg and Mexico City. He summarizes (page 245) a few geometrical properties about the stereographic projection : a circle on the sphere will be transformed in a circle on the plane. Then (page 249), he connects the parallax to the Earth mass through the “knowledge of [gravitational] attraction”  (it should be noted that, p. 249, the word "increases" should be replaced by "decreases").

Cassini de Thury 1757, HMARS 1757 p. 326-335 [[ HMARS-1757 p.326-335 ]]

César-François Cassini de Thury, called Cassini III, (1714-1784) focused his interest on the choice of the observing sites for the 1761 missions of the Science Academy, as well as the instruments to be used to observe the internal contacts of the transit in the best way possible.

Ferguson 1760, A plain method [[ 1605-(001 à 055) ]]

The English James Ferguson (1710-1776) published in 1760 (here, 3rd edition of 1764) an outstanding study of the 1761 transit, with an explanation of the Halley method (page 316) [[014 ]] . He extensively describes a graphic method than can be followed step by step (page 329) [[ 029 ]] with the help of figure xvi [[  028 ]] to determine the parallax effect during the transit. He estimates the precision to 1/400 (page 340) [[040  ]].

The map (figure xvii) [[043> ]] indicates the instants of internal contacts in every places on Earth, at the London time, which were computed assuming a solar parallax of 10.5”.

Le Gentil 1760, Journal des Sçavans (mars 1760) p. 132-141 [[JdS-1760 p.132-142 ]]

Guillaume Le Gentil de la Galaisière (1725-1792) first summarizes the state of knowledge about transits. He quotes Horrocks (Horroxe), Kepler, Gassendi, Lansberge (1561-1632) and then Halley, and explains his method.

Then, Le Gentil indicates he is sent in mission in Pondichéry, India (where the Oriental India Company took place, near Madras, by then) by the Royal Academy of Science (page 319). He computed (page 141) that the parallax effect there should be of about 6 minutes (given a solar parallax of 10") for the coming in and out of the center of Venus’ disc.

Pondichéry, port view, print [[ Compagnie-des-Indes-221484 ]]

Pondichéry, on east cost of India, where the “Compagnie française des Indes orientales” (the French company of Oriental India) takes place. The Royal Academy of Sciences has sent Le Gentil there to observe the 1761 transit.

Trébuchet 1760, Journal des Sçavans (mars 1760) p. 142-144 [[ JdS-1760 p.142-144 ]]

Claude-Etienne Trébuchet (1722-1784) was a student of Joseph-Nicolas Delisle (1688-1768) who extensively worked on the Mercury and Venus transits of 1761. Trébuchet explained two geometric mistakes Halley did in his Memorandum of 1716. This errors were already mentioned in the Mémoires de l'Académie des Sciences pour 1757.

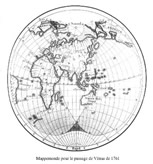
Delisle, world map, Venus 1761

Joseph-Nicolas Delisle (1688-1768) draws a world map indicating the visibility zones of the Venus transit of June 6, 1761 in Asia, and then in Europe and Africa.

Map : The 7-years war [[ carte-1758-64415 ]]

During the 7-years war (1756-1763), France and allies are opposed to the English and Prussian coalition on the sea and in the colonies. When the Paris treaty was signed (1763), English ruled the seas.

Observations of 1761

Anonymous, HMARS 1761, p. 98-117 (History part) [[ HMARS-1761 p.98-117 ]]

This pages are a good summary of the different observations performed in 1761, in France and abroad. The comparison of the measurements allow to bracket the solar parallax value between 9" and 10".

Various authors 1761, HMARS 1761, p. 65-486 (Memorandum Part)

This compilation of the Royal Academy of Science memoranda of the year 1761 encompasses a great number of reports on observations of the June 6, 1761 transit. The most noteworthy are :

- Cardinal de Luynes at Sens [[ HMARS-1761 p.65-71 ]],

- Le Monnier (1715-1799) at the Saint-Hubert castle, near Rambouillet, in the company of king Louis XV [[ HMARS-1761 p. 72-76 ]],

- Maraldi at Paris Observatory ; G.-D. Maraldi (1709-1788) is the grand-nephew of Jean-Dominique Cassini [[ HMARS-1761 p. 76-77 ]],

- Lacaille (1713-1762) at Conflans-sous-Carrières (= Charenton, near Paris) [[ HMARS-1761 p. 78-81 ]],

- Lalande at Luxembourg palace noticed (p. 84) the "black drop" phenomenon [[ HMARS-1761 p. 81-86 ]],

- Le Monnier and then Lalande computed the parallax value by the combination of Paris and Rodriguez Island observations [[ HMARS-1761 p. 88-89 ]],

- Grandjean de Fouchy (1707-1788), at La Muette (Paris), at the physics chamber of the king ; he noticed (p. 100) the elongation of Venus’ disc during the second internal contact [[ HMARS-1761 p. 96-105 ]],

- Lalande indicated that his calculations published in La Connaissance des Temps pour 1761 (the knowledge of times for 1761) are late by “more than half an hour” compared to the observations, due to still inaccurate corrections performed on Halley tables [[ BdL/1à12.html ]], [[ HMARS-1761 p. 107-111 ]],

- Chappe’s journey to Tobolsk (Siberia) with his Venus transit observations (p. 360), (see next),

- Calculations of the solar parallax by Pingré (see next, in the data analysis part).

Chappe 1761, HMARS 1761 p. 337-377 [[ HMARS-1761 p.337-372 ]], [[ HMARS-1761 p.373-377 ]]

Jean Chappe d'Auteroche (1728-1769) describes his mission in Siberia. His report on his winter journey through Vienna, Saint Petersburg and Moscow (5000 km in almost 5 months) encompasses interesting geographical and ethnological aspects.

Chappe first determined the geographical coordinates of Tobolsk. The partial Sun eclipse of June, 3 allowed him to obtain the longitude of the place (4h 24min 12s east of Paris) because Jupiter was too low on the horizon, shorter before sunrise (by then, longitudes were mainly obtained thanks to the observation of Jupiter satellites).

The Venus transit observation is outstanding : the duration between the two internal contacts is close from 15s to the value obtained from modern calculations. Chappe extensively describes the presence of a ring around Venus, which sometimes shows as a croissant (Figure p. 377). Measurements of Chappe are with no doubts the best performed in 1761 for the Venus transit.

Chappe in Tobolsk, painting [[ Chappe-2701bd ]]

Jean Chappe d'Auteroche (1728-1769) observing in Tobolsk (Siberia). The instrument represented on this painting is a quadrant (90° aperture).

Wargentin 1761, Ph.tr. 52, p. 208-213 [[Ph.tr.-52 p.208-213 ]]

Pehr Wargentin (1717-1783) observing in Stockholm. He described (p. 213) an optical phenomenon during the second internal contact that might be due to the presence of an atmosphere around Venus.

Wargentin 1761, Ph.tr. 52, p. 213-216 [[ Ph.tr.-52 p.213-216 ]]

Wargentin describes various observations of the 1761 transit performed in Sweden and Finland. Abo (= Turku) is the former capital of Finland. Hernösand is located close to the Botnie gulf.

Lalande 1761, Ph.tr. 52, p. 216-220 [[ Ph.tr.-52 p.216-220 ]]

Jérôme de Lalande transmits a summary of his observations performed in Paris at the Luxembourg palace, to the Royal Society.

Ferner 1761, Ph.tr. 52, p. 221-225 [[ Ph.tr.-52 p.221-225 ]]

Benedict Ferner (1724-1802), astronomer at Upsala (Sweden), came to France to observe with Fouchy at the Saint-Hubert castle (near Rambouillet) in the company of king Louis XV (see HMARS 1761, p. 96) [[ HMARS-1761 p.72-76 ]]. He presents here various observations performed in and near Paris  ; he describes (p. 223) a “glimmer” around Venus during the second internal contact.

We can notice that Father Noël (p. 222) is a Dominican, physicist of the king.

Planman 1761, Ph.tr. 52, p. 231 [[ Ph.tr.-52 p.231 ]]

Anders Planman (1724-1803) observing at Cajaneburg (nowadays called Kajaani in Finland).

Pingré 1761, Ph.tr. 52, p. 371-377 [[Ph.tr.-52 p.371-377 ]]

Alexandre Pingré (1711-1796) observed at Rodriguez Island, in the Indian Ocean, 600 km east of the Ile-de-France (nowadays called Mauritius). The observations of the first internal contact shortly after sunrise failed because of a cloudy weather.

Bradley, portrait

James Bradley (1693-1762), who succeeded to Halley as a Greenwich Royal Astronomer in 1743, had already discovered the light aberration (1727) and the earth axis nutation (1748). He was one of the main person in charge of the calculations during the English missions for the 1761 transit.

Maskelyne, portrait

Nevil Maskelyne (1732-1811) observing in Saint-Helen Island. When Bradley died in 1762, Maskelyne became Royal Astronomer.

Fort St George in Madras, print [[ pu1845 ]]

The English company of oriental India has a agency near Madras. There, Hirst observed the transit of 1761.

Mason and Dixon, print [[ Mason-Dixon-26772bd ]]

Charles Mason (1728-1786) and Jeremiah Dixon (1733-1779) observed the transit of 1761 at the Cape of Good Hope where only the planet coming out of the Sun’s disc was observable.

As astronomers and geodesians, they drew in 1763 the "Mason and Dixon Line" which delimits the Pennsylvania and Maryland states along a geographical parallel that goes across the Appalachian Mounts.

Rumovsky 1762, Brevis Expositio [[ 20269-5 (001 à 028) ]]

The Russian Stefen Rumovsky (1734-1815) observed at Selenginsk, in Siberia, 200 km east of Irkoutsk, near the Baykal lake. His results are described in French by Pingré in the “Mémoires de l'Académie des Sciences” (Reports of the Science Academy) for 1764 [[ HMARS 1764 p.115-116 ]] and [[ HMARS 1764 p.339-343 ]].

[20 269 (5)] Rumovsky Stephen, Brevis Expositio observationum occasione transitus Veneris per solem in urbe Seleginsk anno (1761) instituterum, 1762, in 4°, in Latin.

Hell 1762, Transitus Veneris [[ 20659-1 (001à021) ]] and [[20205 (001à137) ]]

Maximilien Hell (1720-1792) observed the transit of 1761 in Vienna (Austria). He went to Vardö (North of Norway) for the transit of 1769.

[20659(1)] Hell Maximiliano, Transitus Veneris per discum Solis, anni 1761  ; calculis definitus et methodis observandi illustratus, Vindobanae, no date. Latin Text(18 p).

[20205] Hell Maximiliani, Observatio transitus Veneris ante discum Solis die 5ta Junii 1761…. Observationi bus ejusdem transitus Veneris factis à variis per Europam Viris in observando exercitatis, cum Appendice aliarum nullarum observationum », Vindobonae, s.d. Latin text (124 p).

Heinsius 1764, De Venere [[ 2188-(001à030) ]]

The Danish Gottfried Heinsius (1709-1769) observing in Leipzig.

[2188] Heinsio, G., De Venere in Sole visa, Lipsiae anno 1761, d. 6 Iuni, styl nov horis matutionis temp civili, Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae, [Saint-Petersbourg], X, 1764, Latin text (28 pages)

Le Gentil 1779, Journey [[ 2221-1-(0001à0753) ]] and [[ 2221-2-(0001à0894 ]]

Astronomer at the Academy, Guillaume Hyacinthe Le Gentil de la Galaisière (1725-1792) extensively described his scientific and geographic observations (more than 1600 pages in 2 volumes) during his 11 years trip to the Indian Ocean, from 1760 to 1771.

Among his astronomical observations, he noted several Sun and Moon eclipses as well as an occultation of Antares on October 10th, 1763 (tome 2, p. 589 and Figure on Plate 10) [[ 2221-2-0605 ]] and [[2221-2-0890 ]] . Le Gentil used this data to determine the geographical coordinates of his observatory of Foulpointe (Madagascar). The inclination of the magnetized needle is extensively measured. These measurements are useful for navigation matters. Please refer to the indexes at the end of each volume (13 and 16 pages) [[ 221-1-0725 ]] and [[ 221-2-0861  ]].

[2221, tome 1] et [2221, tome 2] Le Gentil, Voyage dans les mers de l'Inde (Journey to the Indian seas), ordered by the king on the occasion of the Venus transits of June 6 1761, and June 3, 1769. By M. Le Gentil, from the Royal Academy of Sciences. Paris, 1779 and 1781, (2 volumes, 1620 p).

1761 observations analysis

Lalande 1764, Astronomy [[5098-02 (001 à 055) ]]

This Astronomy treatise (1764) is of high scientific level. In Book 11, Lalande describes transits of Venus and Mercury, the methods to predict them and how to determine parallaxes. Lalande observed the coming of Venus out of the Sun’s disc during the 1761 transit in Paris. He computed the solar parallax by the combination of the observations from Pingré (Rodriguez Island), Chappe (in Tobolsk) and from the English Mason (at Cape of Good Hope). He found a parallax of 9" (p. 800).

The great ellipse (Fig. 126) and the abacus (Fig. 131, plate xii page 805) [[ 053 ] ]] allow to graphically determine the parallax effect in any place on Earth. Plate xiv [[ 055  ]] represents a sextant (1/6 of a circle) with drawings from Paris and Greenwich Observatories.

[5098(2)] Lalande, J. J. L. de, Astronomie, tome II, Paris, 1764. French text (52 pages).

Pingré 1761, HMARS 1761 p. 413-486 [[ HMARS-1761 p. 413-433 ]], [[ HMARS-1761 p. 433-439 ]], [[ HMARS-1761 p. 439-450 ]]), [[ HMARS-1761 p. 450-483 ]], [[ HMARS-1761 p. 483-486 ]]).

Alexandre Pingré (1711-1796) observed in the Rodriguez Island (Indian Ocean). He details here the observations performed in various sites in order to determine the solar parallax he assumed to be equal to 10" (p. 450). He successively used three methods of calculation (p. 456). It is worth noting that in 1761, the longitude difference between Paris and Greenwich was still 9 min 10 s (p. 472) instead of 9 min 21 s. This bad knowledge of longitudes is one of the main reasons why the solar parallax determination from Venus transits was so poor. Pingré concluded to a mean value of the solar parallax of 10.60” (p. 486).

Short 1761, Ph.tr. 52, p. 611-628 [[ Ph.tr.-52 p.611-628 ]]

James Short (1710-1768) used various observations performed in Europe and at Cape of Good Hope to determine the solar parallax he assumed to be equal to 8.5" (p. 614). In the table (p. 615), the D.M. acronym means "difference of meridians" or longitude difference, expressed in duration (hours, minutes and seconds of time).

James Short compared instants of the second internal contact (during the coming out of the planet), observed in various sites. He concluded that the parallax is 8.69" (p. 618) then 8.65" (p. 621). He provides the table of geographical coordinates (p. 624) he used in his calculations. It is worth noting that Paris is supposed to be located at 9 min 10 s east of Greenwich (instead of 9 min 21 s). Longitudes are almost correct up to about 0.3°. Western sites in America, like St John's Newfoundland or Jamaica will be chosen as observing sites for the 1769 transit.

Daval 1763, Ph.tr. 53, p. 1-2 [[ Ph.tr.-53 p.1-2 ]]

After James Short determined a solar parallax equal to 8.65" (Ph. tr. 1761, p. 621), Peter Daval computed the Sun’s distance and found about 94.4 millions miles. It is interesting to note the 9 significant digits...

Short 1763, Ph.tr. 53, p. 300-345 [[ Ph.tr.-53 p.300-345 ]]

James Short (1710-1768) has completed his previous report (Ph. tr. 52, p. 611-628) and computed a solar parallax using the 8.5" value hypothesis :

- using the instant of the second internal contact (before the coming out) : 8.57" (p. 326),

- using the duration between two internal contacts, observed from only 8 sites : 8.61" (p. 331),

- using the minimum distance between the centres of Venus and the Sun’s discs : 8.56" (p. 334).

He concluded a value of 8.56" with a 1 % uncertainty (p. 340) although Halley targeted a 0.2 % (1/500) uncertainty. Short was obliged to correct (or "modify") some values of the measured instants or some values of the longitudes. He next describes two geometrical methods to determine the minimum distances of the centres of the Venus and Sun’s discs from the transit duration (p. 343 to 344). The first method is not correct, as the velocity of the motion of Venus along the chord is not constant.

Hornsby 1763, Ph.tr. 53, p. 467-495 [[ Ph.tr.-53 p.467-495 ]]

Thomas Hornsby (1733-1810), professor in Oxford, computed the solar parallax using a value of 9", by the use of the three usual methods (total duration of the transit, minimum distances of the discs centres and internal contacts instants difference).

Mercury transits of 1723, 1736, 1743 and 1753 allowed to improve the longitudes determinations (p. 482). Hornsby concluded to a parallax value of 9.7" (p. 494). Pingré appreciated this report in 1765.

Pingré, HMARS 1765 p. 1-34 [[ HMARS-1765 p.1-34 ]]

This memorandum from Alexandre Pingré (1711-1796) is a long criticism of the memorandum from Short [[ Ph.tr. 53, p. 300-345 ]], which is not explicitly named before page 24. This criticism is focused on the inaccuracies of the longitudes or instants used by James Short that are modified during the calculations without any obvious reasons. Pingré assumed again a parallax of 10" and concluded to a new value of 10.1", using the observations recently received from Pekin (p. 32). Pingré added as a post scriptum (p. 33) that he appreciates Hornsby’s memorandum [[Ph.tr. 53, p. 467-495 ]].

Newcomb 1891, Astronomical Papers [[ 2929 (0001à0137) ]]

The American Simon Newcomb (1835-1909) realised a huge work around 1890. He reconsidered all observations from the transits of 1761 and 1769, using better longitudes determinations. He extensively studied the instruments used and estimated the corresponding uncertainties. He analysed the results obtained and concluded, through an adapted mathematical process, to a value of the solar parallax of 8.79" +/- 0.05" (p. 402) [[ 0134 ]] corresponding to a precision smaller than 0.6 %. The 1761 observations are described from p. 269 to 295.

[2929] Newcomb Simon, Astronomical Papers prepared for the use of the American Ephemeris and Nautical Almanac, vol II, , 1891, Part V., Discussion of observations of the transit of Venus in 1761 and 1769. English text (136 p).