Ouvrages sur le passage de Vénus de 1761

Préparation des observations du passage de 1761

Observations de 1761

Traitement des observations de 1761

Préparation des observations du passage de 1761

Gregory 1663, Scholium [[gregory-p130]]

L'Ecossais James Gregory (1638-1675) publie en 1663 un traité d'optique "avancée" (Optica promota). Au détour d'une simple remarque (Scholium) à la fin de la proposition 87, il évoque la possibilité de déterminer la parallaxe solaire : "Ce problème peut avoir une très belle application, mais peut-être difficile, à partir des observations de Vénus ou de Mercure quand ils obscurcissent une toute petite partie du Soleil [lors d'un passage]. Cela peut conduire en effet à rechercher la parallaxe du Soleil."

Halley

Envoyé en mission en 1677 à l'île de Sainte-Hélène pour y observer le passage de Mercure, le jeune Edmond Halley (1656-1743) est le premier à observer un tel passage en entier. Reprenant l'idée suggérée par Gregory en 1663, il envisage alors une méthode pour déterminer la parallaxe solaire à partir des durées observées depuis deux lieux très éloignés.

En 1716, il publie le texte "fondamental" sur lequel s'appuieront tous les observateurs. Ce texte en latin (Methodus singularis, qua Solis parallaxis sive distantia a Terra ope Veneris intra Solem conspiciendae tuto determinari poterit = "Méthode singulière pour déterminer précisément la parallaxe du Soleil ou sa distance à la Terre par les observations de Vénus dans le Soleil"), ne comporte que les résultats de ses calculs. La précision doit atteindre 1/500 (quingentesimam p. 455) car, selon lui, la durée entre les deux contacts intérieurs peut être déterminée "à moins de 1 s près" (etiam absque errore unius minuti secundi temporis p. 457). Comme il sera mort en 1761 (nobis vita functis p. 460), il en appelle à tous les astronomes anglais, français, et hollandais (p. 460). En supposant la parallaxe solaire égale à 12,5" (duodecim secundorum cum semisse p. 456), il calcule que les durées de passage pourront différer de 17 minutes (septendecim minutis p. 459) entre Port Nelson (90° à l'Ouest de Londres) et le delta du Gange (90° à l'Est).

On présente ici trois versions de ce texte important : l'original de Halley, en latin (1716), une traduction en anglais (1760), une traduction en français (2003).

Halley 1716 (en latin) [[Ph.tr.-29, 1716, p. 455-464]] (la page 454 est manquante, lire ci-dessous le début du texte retranscrit).

Le début du texte latin, en bas de la page 454, est le suivant :

Methodus singularis, quâ Solis Parallaxis sive distantia à Terra, ope Veneris intra Solem conspiciendae, tuto determinari poterit : proposita coram Regia Societate ab Edm. Halleio J.U.D. ejusdem Societatis Secretario.
Plurima sunt maxime quidem paradoxa, omnemque fidem apud vulgus superantia, quae tamen adhibitis. Mathematicarum Scientiarum principiis levi negotio enodantur. Ac sane nullum problema magis arduum ac difficile videbitur, quam est Solis à Terra distantiam vero proximam determinare ; quod tamen obtentis accuratis /
(455) quibusdam observationibus... [[ Ph.tr.-29p.455-464 ]]et schéma [[ Ph.tr.-29p.428-428b]]

Halley 1716 (Ferguson, en anglais) [[ 1605-(014 à 026) ]]
Le texte de Halley a été traduit en anglais et publié en 1760 par James Ferguson (1710-1776) dans son livre "Astronomy" (voir tout l'article III, pages 316 à 327). Ferguson corrige le schéma initial de Halley en dessinant la trajectoire apparente de Vénus inclinée correctement de 14° 38' sur l'équateur (au lieu de 2° 18' pour Halley) et utilise quelques notations différentes. A noter une erreur typographique (page 325, ligne 20) : lire 14' 41" au lieu de 14' 4". Le livre de Ferguson, qui contient beaucoup d'autres informations sur les passages de Vénus, est présenté un peu plus loin.

1605] Ferguson James, Astronomy explained upon Sir Isaac Newton’s principles, and made easy to those who have not studied mathematics. A plain method of finding the distances of all the planets from the sun, by the transit of Venus over the Sun’s disc, in the year 1761. 3rd edition, London, 1764. Texte en anglais (502 pages).

Halley 1716 (en français) [[ Halleytrad ]] Aucune traduction française du texte de Halley n'avait encore été publiée. Cela s'explique d'abord par le fait que les astronomes français qui ont préparé les observations du passage de 1761 lisaient très bien le latin, et n'avaient pas besoin d'une traduction complète ; ensuite par l'évolution des méthodes de calcul de la parallaxe depuis 1716, différentes de celle utilisée par Halley. On trouvera ici une traduction complète du texte latin en français. Le schéma joint [[ fichier-schema-halley-fr.]] est une traduction en français de celui de l'article original de Halley.

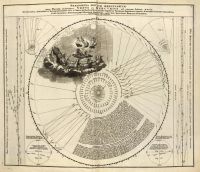
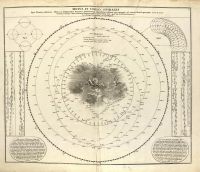
Doppelmayer 1742, Atlas [[ 00047-(003à005) ]]

L'Allemand Johann Gabriel Doppelmayer (1671-1750), publie en 1742 à Nüremberg un recueil de plusieurs diagrammes astronomiques Atlas novus coelestis. Sur la planche 7 (Phaenomena motuum irregularium) [[ 003 ]], il dessine les orbites héliocentriques de Mercure, de Vénus et de la Terre, avec les boucles de rétrogradation pour 1710 (conjonctions inférieures avec le Soleil) et présente les schémas du passage de Vénus attendu en 1761 (fig. iii) et celui de Mercure en novembre 1710 (fig. iv) en réalité, invisible en Europe. La planche 9 (Motus in coelo spirales) [[ 004 ]] présente les orbites géocentriques du Soleil, de Mercure et de Vénus, montrant bien leurs variations de distance de la Terre. Doppelmayer dessine plusieurs boucles de rétrogradation pour Mercure en 1712 (les 5 février, 6 juin et 6 octobre 1712) et pour Vénus (20 juin 1713 et 27 janvier 1715). Ces dernières sont les deux petites boucles les plus proches de la Terre, figurée au centre du schéma. Sur le dessin allégorique, Mercure (à droite) et Vénus (à gauche) sont sur des balançoires, poussées par le Soleil... La fig. 9 de la planche 13 [[ 005 ]] n'est pas une bonne reproduction du dessin de Horrocks du passage de Vénus en 1639 : la planète est mal positionnée sur le disque du Soleil.

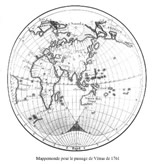
[00047] Doppelmayer J. G., Atlas novus coelestis, Nüremberg, 1742, en latin.

Delisle, mappemonde Mercure 1753

Joseph-Nicolas Delisle (1688-1768) dessine une carte du monde traduisant la visibilité du passage de Mercure le 6 mai 1753, en Asie puis en Europe et en Afrique.

Delisle, manuscrits 1753 et 1760 [[ A-3-12-34b-(001à039) ]]

Manuscrit du mémoire lu à l'Académie en 1760 : "La Description et l'usage de la mappemonde dressée pour le passage de Vénus sur le disque du Soleil qui est attendu le 6 juin 1761".

Un autre manuscrit [[ A-3-12-34b-(037) ]], daté du 6 mai 1753 : "Avis très importants aux astronomes sur le passage de Vénus au devant du Soleil qu'ils attendent le 6 juin 1761".

 

[A-3-12-34b] Delisle, Manuscrits 1753 et 1761 : Mémoires sur le passage de Vénus de 1761.

Anonyme, HMARS 1757 p. 77-99 (partie Histoire) [[ HMARS-1757 p.76-99 ]]

Ces pages retracent l'histoire des passages antérieurs de Mercure et de Vénus, et décrivent les préparatifs des missions pour 1761, avec notamment les choix des sites de Tobolsk et de l'île Rodrigue (p. 89 à 93). Les calculs de Lalande prévoyaient un écart de 17 minutes entre les instants du premier contact intérieur, observé à La Mecque, et à l'île de Pâques, deux sites presque aux antipodes l'un de l'autre (p. 88). En réalité, le passage eut lieu pendant la nuit à l'île de Pâques.

Lalande 1757, HMARS 1757 p. 232-253 [[ HMARS-1757 p.232-253 ]]

Joseph-Jérôme de Lalande (1732-1807) s'est particulièrement investi dans la prévision des passages de 1761 et de 1769. En 1757, il publie un Mémoire sur les passages de Vénus, décrivant la méthode graphique qui permet de déterminer l'effet de parallaxe sur la durée du passage de Vénus. Il suppose la parallaxe solaire égale à 10" (p. 234). Il dessine ensuite (p. 239) une mappemonde en y indiquant par quelques arcs les valeurs de la parallaxe, permettant une lecture directe, sans calculs.

Pour le passage de 1769, Lalande prévoit (p. 244) que les écarts les plus grands se produiront vers (Saint) Petersbourg et vers Mexico. Il rappelle (p. 245) quelques propriétés géomé­triques de la projection stéréographique : un cercle de la sphère se transforme en un cercle sur le plan. Enfin (p. 249), il relie la parallaxe à la masse de la Terre par la "connaissance de l'attraction" gravitationnelle (à noter que, p. 249, le mot "augmentera" est à corriger en "diminuera").

Cassini de Thury 1757, HMARS 1757 p. 326-335 [[ HMARS-1757 p.326-335 ]]

César-François Cassini de Thury, dit Cassini III, (1714-1784) s'intéresse au choix des sites pour les missions de l'Académie des sciences en 1761, ainsi que des instruments à utiliser pour observer le mieux possible les contacts intérieurs.

Ferguson 1760, A plain method [[ 1605-(001 à 055) ]]

L'Anglais James Ferguson (1710-1776) publie en 1760 (ici, 3e édition de 1764) une remarquable étude sur le passage de 1761, expliquant la méthode de Halley (p. 316) [[ 014 ]]. Il décrit longuement une méthode graphique que l'on suit pas à pas (p. 329...) [[ 029 ]] à l'aide de la planche xvi [[ 028 ]] pour déterminer l'effet de parallaxe sur la durée du passage qu'il estime pouvoir obtenir avec une précision de 1/400 (p. 340) [[ 040 ]].

La carte (planche xvii) indique les instants des contacts internes en tout point de la Terre, en heure de Londres, calculés en supposant la parallaxe solaire égale à 10,5".

[1605] Ferguson James, Astronomy explained upon Sir Isaac Newton’s principles, and made easy to those who have not studied mathematics. A plain method of finding the distances of all the planets from the sun, by the transit of Venus over the Sun’s disc, in the year 1761. An account of Mr. Horrox’s observation of the transit of Venus in the year 1639 ; and of the distances of all the planets from the Sun, as deduced from observations of the transit in the year 1761, 3rd edition, London, 1764. Texte illustré en anglais (502 pages).

Le Gentil 1760, Journal des Sçavans (mars 1760) p. 132-142 [[ JdS-1760 p.132-142 ]]

Guillaume Le Gentil de la Galaisière (1725-1792) résume d'abord l'état des connaissances sur les passages. Il cite Horrocks (Horroxe), Kepler, Gassendi, Lansberge (1561-1632) puis Halley, expliquant la méthode.

Le Gentil indique ensuite qu'il doit de rendre en Inde à Pondichéry (alors siège de la Compagnie des Indes orientales, près de Madras), envoyé en mission par l'Académie royale des Sciences (p. 139). Il calcule (p. 141) que l'effet de parallaxe y sera de près de 6 minutes (si la parallaxe solaire vaut 10") pour l'entrée et la sortie du "centre" de Vénus.

Pondichéry, vue du port, gravure [[ Compagnie-des-Indes-221484 ]]

Pondichéry, sur la côte Est de l'Inde, est le siège de la Compagnie française des Indes orientales. L'Académie royale des sciences charge Le Gentil d'y observer le passage de 1761.

Trébuchet 1760, Journal des Sçavans (mars 1760) p. 142-144 [[ JdS-1760 p.142-144 ]]

Claude-Etienne Trébuchet (1722-1784) a été un élève de Joseph-Nicolas Delisle (1688-1768) lequel a beaucoup travaillé sur les passages de Mercure et de Vénus pour 1761. Trébuchet explique deux erreurs géométriques dans le mémoire de 1716 de Halley, erreurs déjà signalées dans les Mémoires de l'Académie royale des sciences de 1757.

Delisle, mappemonde Vénus 1761

Joseph-Nicolas Delisle (1688-1768) dessine une carte du monde traduisant la visibilité du passage de Vénus le 6 juin 1761, en Asie puis en Europe et en Afrique.

Carte : Guerre de Sept-Ans [[ carte-1758-64415 ]]

Pendant la guerre de Sept-Ans (1756-1763), la France et ses alliés sont opposés, sur mer et aux colonies, à la coalition de l'Angleterre et de la Prusse. Lors du traité de Paris (1763), les Anglais sont désormais maîtres des mers.

Observations de 1761

Anonyme, HMARS 1761, p. 98-117 (partie Histoire) [[ HMARS-1761 p.98-117 ]]

Ces pages constituent une très bonne synthèse des différentes observations effectuées en 1761, tant en France qu'à l'étranger. La comparaison des mesures permet de calculer que la parallaxe solaire est comprise entre 9" et 10".

Auteurs divers 1761, HMARS 1761, p. 65-486 (partie Mémoires)

Ce recueil des Mémoires de l'Académie royale des sciences de 1761 contient de nombreux mémoires sur les observations du passage du 6 juin 1761. Parmi les plus intéressants, on trouve :

- le cardinal de Luynes à Sens [[ HMARS-1761 p.65-71 ]],

- Le Monnier (1715-1799) au château de Saint-Hubert, près de Rambouillet, en présence du roi Louis XV [[ HMARS-1761 p. 72-76]],

- Maraldi à l'Observatoire de Paris ; G.-D. Maraldi (1709-1788) est un petit-neveu de Jean-Dominique Cassini [[ HMARS-1761 p. 76-77]],

- Lacaille (1713-1762) à Conflans-sous-Carrières (= Charenton, près de Paris) [[ HMARS-1761 p. 78-81]],

- Lalande au Palais du Luxembourg signale (p. 84) le phénomène dit de "la goutte noire", [[ HMARS-1761 p. 81-86]],

- Le Monnier puis Lalande calculent la parallaxe en combinant les observations à Paris et à l'île Rodrigue [[ HMARS-1761 p. 88-89]],

- Grandjean de Fouchy (1707-1788), à La Muette (Paris), au cabinet de physique du roi ; il signale (p. 100) l'allongement du disque de Vénus lors du 2e contact interne [[ HMARS-1761 p. 96-105]],

- Lalande signale que les calculs qu'il a publiés dans La Connaissance des Temps pour 1761 sont en retard de "plus de demi-heure" sur l'observation, à cause des corrections encore imparfaites des Tables de Halley [[ BdL/1à12.html ]], [[ HMARS-1761 p. 107-111]],

- le voyage de Chappe à Tobolsk en Sibérie avec ses observations du passage de Vénus (p. 360), (voir ci-après),

- calculs de la parallaxe solaire par Pingré, p. 413 à 486 (voir l'explication plus loin, dans le traitement des observations).

Chappe 1761, HMARS 1761 p. 337-377 [[ HMARS-1761 p.337-372 ]], [[ HMARS-1761 p.373-377 ]]

Jean Chappe d'Auteroche (1728-1769) décrit sa mission en Sibérie. Le récit de son voyage en hiver, passant par Vienne, Saint-Petersbourg et Moscou (5000 km en près de 5 mois) contient des aspects géographiques, historiques et ethnographiques intéressants.

Chappe détermine d'abord les coordonnées de Tobolsk. L'éclipse partielle de Soleil du 3 juin lui permet d'obtenir la longitude (4h 24m 12s à l'Est de Paris) car Jupiter n'y est visible qu'au ras de l'horizon, peu avant le lever du Soleil (les longitudes étaient généralement déterminées par l'observation des phénomènes des satellites de Jupiter).

L'observation du passage de Vénus est remarquable : la durée entre les deux contacts internes est correcte à 15 s près, comparée aux calculs modernes. Chappe décrit longuement la présence d'un anneau autour de Vénus, prenant parfois la forme d'un croissant (schéma p. 377). Les mesures de Chappe sont sans doute les meilleures réalisées en 1761 pour le passage de Vénus.

Chappe à Tobolsk, peinture [[ Chappe-2701bd ]]

Jean Chappe d'Auteroche (1728-1769) observe à Tobolsk (Sibérie). L'instrument représenté sur cette peinture est un quart-de-cercle (90° d'ouverture).

Wargentin 1761, Ph.tr. 52, p. 208-213 [[ Ph.tr.-52 p.208-213 ]]

Pehr Wargentin (1717-1783) observe à Stockholm. Il décrit (p. 213) un phénomène optique lors du 2e contact interne, peut-être dû à la présence d'une éventuelle atmosphère autour de Vénus.

Wargentin 1761, Ph.tr. 52, p. 213-216 [[ Ph.tr.-52 p.213-216 ]]

Wargentin décrit diverses observations du passage de 1761 effectuées en Suède et en Finlande. Abo (= Turku) est l'ancienne capitale de la Finlande. Hernösand est située au bord du golfe de Botnie.

Lalande 1761, Ph.tr. 52, p. 216-220 [[ Ph.tr.-52 p.216-220 ]]

Jérôme de Lalande transmet à la Royal Society un résumé des observations faites à Paris au Palais du Luxembourg.

Ferner 1761, Ph.tr. 52, p. 221-225 [[ Ph.tr.-52 p.221-225 ]]

Benedict Ferner (1724-1802), astronome à Uppsal (Suède), est venu en France observer avec Fouchy au château de Saint-Hubert (près de Rambouillet) en présence du roi Louis XV (voir HMARS 1761, p. 96) [[ HMARS-1761 p.72-76 ]]. Il présente ici diverses observations effectuées à Paris et près de Paris ; il décrit (p. 223) une "lueur" tout autour de Vénus lors du 2e contact intérieur.

A noter que le Père Noël (p. 222) est un dominicain, gardien du cabinet de physique du roi.

Planman 1761, Ph.tr. 52, p. 231 [[ Ph.tr.-52 p.231 ]]

Anders Planman (1724-1803) observe à Cajaneburg (= Kajaani en Finlande actuelle).

Pingré 1761, Ph.tr. 52, p. 371-377 [[ Ph.tr.-52 p.371-377 ]]

Alexandre Pingré (1711-1796) a observé à l'île Rodrigues (Rodrigue en français), dans l'océan Indien, à 600 km à l'Est de l'île de France (qui est l'actuelle île Maurice). Les nuages l'empêchent d'observer le 1er contact interne peu après le lever du Soleil.

Bradley, portrait

James Bradley (1693-1762), successeur de Halley en 1743 comme Astronome royal à Greenwich, avait déjà découvert l'aberration de la lumière (1727) et la nutation de l'axe de la Terre (1748). Il est l'un des principaux "calculateurs" des missions anglaises pour le passage de 1761.

Maskelyne, portrait

Nevil Maskelyne (1732-1811) observe à Sainte-Hélène. Il deviendra Astronome royal en 1762, à la mort de Bradley.

Fort St George à Madras, gravure [[ pu1845 ]]

La Compagnie anglaise des Indes orientales possède un comptoir près de Madras. Hirst y observe le passage de 1761.

Mason et Dixon, gravure [[ Mason-Dixon-26772bd ]]

Charles Mason (1728-1786) et Jeremiah Dixon (1733-1779) ont observé le passage de 1761 depuis le Cap de Bonne-Espérance (où seule la sortie était visible).

En tant qu'astronomes et géodésiens, ils vont tracer en 1763 la "Mason and Dixon Line", limite entre les Etats de Pennsylvanie et du Maryland, le long d'un parallèle géographique, traversant les Monts Appalaches.

Rumovsky 1762, Brevis Expositio [[ 20269-5 (001 à 028) ]]

Le Russe Stephan Rumovsky (1734-1815) observe à Sélenginsk, en Sibérie, 200 km à l'Est d'Irkoutsk, près du lac Baykal. Ses résultats sont décrits (en français) par Pingré dans les Mémoires de l'Académie des Sciences pour 1764 [[ HMARS 1764 p.115-116 ]] et [[ HMARS 1764 p.339-343 ]].

[20 269 (5)] Rumovsky Stephen, Brevis Expositio observationum occasione transitus Veneris per solem in urbe Seleginsk anno (1761) instituterum, 1762, in 4°, en latin.

Hell 1762, Transitus Veneris [[ 20659-1 (001à021) ]] et [[ 20205 (001à137) ]]

Maximilien Hell (1720-1792) observe le passage de 1761 à Vienne (Autriche). Il ira à Vardö (au Nord de la Norvège) pour le passage de 1769.

[20659(1)] Hell Maximiliano, Transitus Veneris per discum Solis, anni 1761 ; calculis definitus et methodis observandi illustratus, Vindobanae, non daté. Texte en latin (18 p).

[20205] Hell Maximiliani, Observatio transitus Veneris ante discum Solis die 5ta Junii 1761…. Observationi bus ejusdem transitus Veneris factis à variis per Europam Viris in observando exercitatis, cum Appendice aliarum nullarum observationum », Vindobonae, s.d. Texte en latin (124 p).

Heinsius 1764, De Venere [[ 2188-(001à030) ]]

Le Danois Gottfried Heinsius (1709-1769) observe à Leipzig.

[2188] Heinsio, G., De Venere in Sole visa, Lipsiae anno 1761, d. 6 Iuni, styl nov horis matutionis temp civili, Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae, [Saint-Petersbourg], X, 1764, texte en latin (28 pages).

Le Gentil 1779, Voyage [[ 2221-1-(0001à0753) ]] et [[ 2221-2-(0001à0894) ]]

L'astronome académicien Guillaume Hyacinthe Le Gentil de la Galaisière (1725-1792) décrit très longuement (plus de 1600 pages en 2 volumes) ses observations scientifiques et géographiques faites lors de son voyage de 11 ans dans l'Océan Indien, de 1760 à 1771.

Parmi les observations astronomiques, il note plusieurs éclipses de Soleil ou de Lune ainsi qu'une occultation d'Antares le 10 octobre 1763 (tome 2, p. 589 et schéma planche 10) [[ 2221-2-0605 ]] et [[ 2221-2-0890 ]] que Le Gentil exploite pour déterminer les coordonnées de son observatoire à Foulpointe (Madagascar). L'inclinaison de "l'éguille (sic) aimantée" est l'objet de nombreuses mesures, utiles pour la navigation. Consulter les index en fin de chaque volume (13 et 16 pages) [[ 2221-1-0725 ]] et [[ 2221-2-0861 ]].

[2221, tome 1] et [2221, tome 2] Le Gentil, Voyage dans les mers de l'Inde, fait par ordre du Roi, à l'occasion du Passage de Vénus sur le Disque du Soleil, le 6 Juin 1761, et le 3 du même mois 1769. Par M. Le Gentil, de l'Académie Royale des Sciences. Paris, 1779 et 1781, (2 volumes, 1620 p).

Traitement des observations de 1761

Lalande 1764, Astronomie [[ 5098-02 (001 à 055) ]]

Ce traité d'Astronomie (1764) est d'un niveau élevé. Dans le livre 11, Lalande décrit les passages de Vénus ou de Mercure sur le Soleil, les manières de les calculer et de déterminer les effets de parallaxe. Lalande a observé la sortie du passage de 1761 depuis Paris. Il calcule la parallaxe solaire en combinant les observations de Pingré (à l'île Rodrigue), de Chappe (à Tobolsk) et de l'Anglais Mason (au Cap de Bonne-Espérance). Il conclut la valeur 9" (p. 800).

La grande ellipse (fig. 126) et l'abaque (fig. 131, planche xii page 805) [[ 053 ]] permettent de déterminer graphiquement l'effet de parallaxe en n'importe quel point de la Terre. La planche xiv [[ 055 ]] décrit un sextant (1/6 de cercle) avec les dessins des observatoires de Paris et de Greenwich.

[5098(2)] Lalande, J. J. L. de, Astronomie, tome II, Paris, 1764. Texte en français (52 pages).

Pingré 1761, HMARS 1761 p. 413-486 [[ HMARS-1761 p. 413-433 ]], [[ HMARS-1761 p. 433-439 ]], [[ HMARS-1761 p. 439-450 ]]), [[ HMARS-1761 p. 450-483 ]], [[ HMARS-1761 p. 483-486 ]]).

Alexandre Pingré (1711-1796) a observé à l'île Rodrigue, dans l'océan Indien. Il traite ici les observations effectuées en divers sites pour déterminer la parallaxe solaire qu'il suppose égale à 10" (p. 450). Il utilise successivement trois méthodes de calcul (p. 456). A noter qu'en 1761, l'écart en longitude entre Paris et Greenwich est encore de 9 min 10 s (p. 472) au lieu de 9 min 21 s. La connaissance peu précise des longitudes sera une des raisons pour lesquelles la détermination de la parallaxe solaire par les passages de Vénus ne donnera pas de très bons résultats. Pingré conclut (p. 486) une parallaxe moyenne de 10,60".

Short 1761, Ph.tr. 52, p. 611-628 [[ Ph.tr.-52 p.611-628 ]]

James Short (1710-1768) traite diverses observations faites en Europe et au Cap de Bonne-Espérance pour déterminer la parallaxe solaire qu'il suppose égale à 8,5" (p. 614). Dans le tableau (p. 615), l'indication D.M. signifie "différence des méridiens" ou différence des longitudes, exprimée en durée (heures, minutes et secondes de temps).

Short compare les instants du 2e contact interne (lors de la sortie), observés en divers sites. Il conclut la parallaxe à 8,69" (p. 618) puis 8,65" (p. 621). Il fournit (p. 624) une table des coordonnées géographiques employées dans ses calculs. On remarque que Paris est supposé situé à 9 min 10 s à l'Est de Greenwich (au lieu de 9 min 21 s). Les longitudes sont assez correctes, à 0,3° près environ. Les sites très à l'Ouest, vers l'Amérique comme St John's Newfoundland (= Terre Neuve) ou la Jamaïque seront des lieux d'observation du passage de 1769.

Daval 1763, Ph.tr. 53, p. 1-2 [[ Ph.tr.-53 p.1-2 ]]

Après que Short ait déterminé la parallaxe solaire à 8,65" (Ph. tr. 1761, p. 621), Peter Daval calcule la distance du Soleil et trouve près de 94,4 millions de miles (1 mile anglais = 1609 m), soit l'équivalent de 152 millions de km. A noter les nombres à 9 chiffres significatifs...

Short 1763, Ph.tr. 53, p. 300-345 [[ Ph.tr.-53 p.300-345 ]]

James Short (1710-1768) reprend et complète son mémoire précédent (Ph. tr. 52, p. 611-628) puis calcule la parallaxe solaire à partir de l'hypothèse 8,5" :

- par l'instant du 2e contact intérieur (avant la sortie) : 8,57" (p. 326),

- par la durée entre les deux contacts intérieurs, observée en 8 sites seulement : 8,61" (p. 331),

- par la distance minimale entre les centres de Vénus et du disque solaire : 8,56" (p. 334),

puis conclut 8,56" à 1 % près (p. 340) alors que Halley pensait obtenir 0,2 % (1/500). Mais Short est amené à corriger (ou "modifier") certaines valeurs des instants observés ou des longitudes. Il décrit ensuite deux méthodes géométriques pour déterminer la moindre distance des centres à partir de la durée du passage (p. 343 et 344), la première n'étant pas correcte car la vitesse de déplacement de Vénus sur la corde n'est pas constante.

Hornsby 1763, Ph.tr. 53, p. 467-495 [[ Ph.tr.-53 p.467-495 ]]

Thomas Hornsby (1733-1810), professeur à Oxford, calcule la parallaxe solaire en supposant 9", au moyen des trois méthodes habituelles, exploitant la durée totale observée, la distance minimale entre les centres, puis l'instant observé du même contact intérieur.

Les passages de Mercure de 1723, 1736, 1743 et 1753 ont permis d'améliorer les déterminations de longitudes (p. 482). Hornsby conclut la parallaxe à 9,7" (p. 494). Ce mémoire a été apprécié par Pingré en 1765.

Pingré, HMARS 1765 p. 1-34 [[ HMARS-1765 p.1-34 ]]

Ce mémoire d'Alexandre Pingré (1711-1796) est une longue critique du mémoire de Short [[ Ph.tr. 53, p. 300-345 ]]qu'il ne nomme pas avant la page 24. La critique porte sur les incertitudes des longitudes ou des instants utilisés, que Short modifie sans toujours en donner la raison. Pingré suppose encore la parallaxe de 10" et, utilisant les observations de Pékin qu'il vient de recevoir, conclut 10,1" (p. 32). Pingré ajoute en post scriptum (p. 33) qu'il apprécie le mémoire de Hornsby [[Ph.tr. 53, p. 467-495 ]].

Newcomb 1891, Astronomical Papers [[ 2929 (0001à0137) ]]

L'Américain Simon Newcomb (1835-1909) réalise un travail considérable vers 1890 en reprenant systématiquement toutes les observations des passages de 1761 et de 1769, à partir de meilleures déterminations des longitudes. Il étudie longuement les instruments utilisés, évalue les incertitudes de l’époque et analyse les résultats obtenus pour conclure, après un traitement mathématique approprié, la parallaxe solaire à 8,79" +/- 0,05" (p. 402) [[ 0134 ]] soit une précision inférieure à 0,6 %. Les observations de 1761 sont décrites p. 269 à 295.

[2929] Newcomb Simon, Astronomical Papers prepared for the use of the American Ephemeris and Nautical Almanac, vol II, , 1891, Part V., Discussion of observations of the transit of Venus in 1761 and 1769. Texte en anglais (136 p).